Journal of Number Theory

Volume 180, Issue 24, 15 December 2010, Pages 4763-4771

Fun with $\F_1$

• Alain Connes ^abc,
• Caterina Consani ^d⁎,
• Matilde Marcolli ^ef

1. ^⁎ Corresponding author.
2. ^a Collège de France, 3, rue d'Ulm, Paris, F-75005 France
3. ^b I.H.E.S., Bures-sur-Yvette, France
4. ^c Vanderbilt University, Nashville, TN, USA
5. ^d Mathematics Department, Johns Hopkins University, 3400 N. Charles Street, Baltimore, MD 21218, USA
6. ^e Max-Planck Institut für Mathematik, Vivatsgasse 7, Bonn D-53111, Germany
7. ^f Mathematics Department, Caltech, 1200 E. California Blvd., Pasadena, CA 91125, USA

Research highlights

Abstract

Video abstract

Research highlights

• This paper provides for the first time a concrete relation between the ideas of R. Steinberg and J. Tits on the limit case of the Galois fields $\F_q$, for $q \to 1$, and the zeros of the Riemann zeta function.
• The bridge is supplied by the quantum statistical mechanical system of J.B. Bost and A. Connes.
• This is a Hecke algebra with a natural time evolution which admits the Riemann zeta function as partition function and also provides a spectral realization of the zeros and a trace formula interpretation of the explicit formulas.
• We show that the Bost-Connes system naturally arises, by extension of scalars, from the "field with one element" $\F_1$ to rational numbers.
• The inductive structure of the abelian part of the endomotive associated to the system corresponds to the tower of finite extensions of $\F_1$, while the endomorphisms refect the Frobenius correspondences.
• We study the reduction of the endomotive and of the corresponding noncommutative crossed product algebra at a rational prime.

Abstract

We show that the algebra and the endomotive of the quantum statistical mechanical system of Bost–Connes naturally arises by extension of scalars from the “field with one element” to rational numbers. The inductive structure of the abelian part of the endomotive corresponds to the tower of finite extensions of that “field,” while the endomorphisms reflect the Frobenius correspondences. This gives in particular an explicit model over the integers for this endomotive, which is related to the original Hecke algebra description. We study the reduction at a prime of the endomotive and of the corresponding noncommutative crossed product algebra.

Video abstract

Video is also available at http://www.youtube.com/watch?v=az_0pxm1jrI.

Play video

1. Introduction

Starting with seminal observations of J. Tits on the classification of simple finite groups (cf. [18]), the a priori vague idea that a suitable analogue of the geometry over the finite fields $\F_q$ should make sense in the limit case “$q=1$” has been taking more and more substance and has given rise to a number of different approaches (cf. [9], [10], [11], [12], [15], [16] and [19]). So far, the relation between these constructions and the Riemann zeta function has remained elusive, in spite of the hope of being able to consider the tensor product $\Z\otimes_{\F_1}\Z$ as a non-trivial analogue of the product of a curve by itself (see [12]).

It is known that the quantum statistical mechanical system of [1] (which we refer to as the BC-system) gives, after passing to the dual system, a spectral realization of the zeros of the Riemann zeta function, as well as a trace formula interpretation of the Riemann-Weil explicit formulas (see [1], [2], [4], [5], [13]).

The main result of the present paper is that the BC-system and the associated algebraic endomotive as defined in [4] appear from first principles, by studying the algebraic extensions of $\F_1$ and implementing the techniques developed in [11] and [16].

In this formalism, a variety (of finite type) over $\F_1$ determines, after extension of scalars to $\Z$, a variety over $\Z$. Moreover, even though the algebraic nature of $\F_1$ is still mysterious, a basic equation of the theory is the formal equality

(1) \[ \F_{1^n}\otimes_{\F_1} \Z:=\Z[T]/(T^n-1)\,, \qquad n\in\N . \]

Our starting point is that the natural inductive structure defined by the extensions $\F_{1^n}\subset \F_{1^m}$, for $n|m$, translates into a natural inductive system of algebras, whose limit is the group ring $\Z[\Q/\Z]$. After tensoring by $\Q$, this group ring is a key ingredient in the definition of the BC-endomotive [4], since it describes the abelian part of the structure. The second key ingredient is the semigroup of endomorphisms of the above algebra associated to the action of $\N$, given by multiplication, in the group $\Q/\Z$. This operation describes an analogue over $\F_1$ of the classical Frobenius correspondence, and part of our investigation is directed at making this statement more precise.

In Section 2 we start our study by recalling the group theoretical and an equivalent geometrical description of the abelian part of the BC algebra. In particular, the sub-section Section 2.1 introduces the relevant abelian algebra, that is the group ring of the abelian group $\Q/\Z$, together with the endomorphisms $\sigma_n$ given by multiplication by $n$ in $\Q/\Z$ as well as their partial inverses $\rho_n$. In Section 2.2 we describe the same space by using elementary techniques of algebraic geometry.

In Section 3 we give an interpretation of the abelian part of the BC-system in terms of a system of pro-affine varieties $\mu^{(k)}$ over $\F_1$ which are defined by considering affine group schemes of roots of unity.

The core of the paper concentrates on the definition of an integral model for the BC-system over $\Q$ and on the generalization of the notion of endomotive that was originally developed over fields of characteristic zero only. This study is motivated by the idea to achieve an interesting link between the thermodynamical system associated to the BC-algebra (and its connection to the zeta-function) and the theory of algebraic varieties over $\F_1$. Working with spaces over $\F_1$ implicitly requires one to define a geometric theory over $\Z$ and thus to set-up a corresponding construction over finite fields (and their extensions), after taking the reduction at the various primes. The main result of Section 4 is that the original noncommutative BC-algebra $\cA_\Q$ has a model over $\Z$.

In Section 4.1 we shortly review the description of the $C^*$-algebra of the BC-system in terms of groupoids and in Section 4.2 we recall the presentation of $\cA_\Q$ by generators and relations. Section 4.3 describes how to eliminate the denominators in the partial inverses $\rho_n$ of the endomorphisms $\sigma_n$. This leads us in Section 4.4 to the definition of the integral model $\cA_\Z$ of the BC-algebra by generators and relations. In Proposition 4.10 and Corollary 4.11 , we show that the general element of $\cA_\Z$ can be uniquely written as a sum of simple monomials labeled by $\Q/\Z\times \Q_+^*$. In Section 4.5 we define an isomorphism of $\cA_\Z$ with the integral version $\cH_\Z(\Gamma,\Gamma_0)$ of the original Hecke algebra of [1], and deduce from that the existence of two different involutions on the rational algebra $\cA_\Q$. In Section 5 we analyze the BC endomotive over a perfect field of characteristic $p$, and we relate the endomorphisms of this system to the Frobenius correspondence.

We isolate the $p$-part $\cC_p$ of the BC-algebra in characteristic $p$ and exhibit its nilpotent nature by constructing in Proposition 5.8 a faithful representation of $\cC_p$ as lower triangular infinite matrices. This representation is obtained by relating the algebra $\cC_p$ to a sub-semigroup of the group of affine transformations of the additive group $S=\cup \frac{1}{p^n}\Z\subset \R$. A new feature that arises in positive characteristic is the appearance of unreduced algebras in the abelian part of the system. We explain the effect of reduction of these algebras in Section 5.3 and briefly discuss in Section 5.4, the required extension of the notion of endomotive to the general (unreduced) framework.

Finally, in Section 6 we prove that the BC system has a model defined over $\F_1$. This result allows us to deduce that the symmetries of the BC system are recovered from the automorphisms of $\F_{1^\infty}=\varinjlim \F_{1^n}$ over $\F_1$. In fact, we show that the BC endomotive embodies the structure of the extensions $\F_{1^n}$ of $\F_1$ through the Frobenius correspondence which is implemented by the action of the endomorphisms on the abelian part of the associated algebra. More precisely, we show that these endomorphisms coincide with the Frobenius correspondence in the reduction of the BC system over a perfect field of positive characteristic. We then use this result to prove that the original analytic endomotive of the BC system can be recovered from the data supplied at infinity in the form of an inductive system of Banach algebras.

2. The abelian part of the BC system and its endomorphisms

In this section we shall give a short overview of two equivalent formulations of the abelian part of the algebra describing the quantum statistical mechanical system introduced in [1] as well as the associated endomotive [4]. In the following and throughout the paper we shall refer to it as the BC-system (cf.  Definition 4.1).

2.1 Group theoretic description

The BC-endomotive over $\Q$ is defined as the algebraic crossed product of the group ring $\Q[\Q/\Z]$ by the action of a semigroup of endomorphisms.

In the following, we denote by $e(r)$, for $r\in \Q/\Z$, the canonical generators of the group ring $\Q[\Q/\Z]$ with presentation

(2) \[ e(a+b)=e(a)e(b)\qqq a, b \in \Q/\Z. \]

We now describe in group theoretic terms the semigroup action on this group ring. Let $\Gamma=\Q/\Z$. For each $n$, let $\Gamma_n\subset \Gamma$ be the $n$-torsion subgroup

(3) \[ \Gamma_n=\{x\in \Gamma\,|\, nx=0\}\,. \]

Proposition 2.1 Let $n\in \N$.

• (a) One has an exact sequence of abelian groups

  (4) \[ 1\to \Gamma_n\to \Gamma\stackrel{\times n}{\to} \Gamma\to 1 . \]

• (b) The operator

  (5) \[ \pi_n=\frac 1n\sum_{s\in\Gamma_n} e(s) \]

  defines an idempotent $\pi_n\in \Q[\Q/\Z]$. One has $\pi_n\pi_m=\pi_k$ where $k$ is the least common multiple of $n$ and $m$.

• (c) The formula

  (6) \[ \rho_n: \Q[\Q/\Z]\to\Q[\Q/\Z],~ \rho_n(e(r))=\frac 1n\sum_{ns=r} e(s) \]

  defines an endomorphism of $\Q[\Q/\Z]$. Moreover $\rho_n$ is a ring isomorphism between $\Q[\Q/\Z]$ and the reduced algebra by $\pi_n$, more precisely one has

  (7) \[ \rho_n: \Q[\Q/\Z]\stackrel{\sim}{\to}\pi_n\Q[\Q/\Z]\,, \ \rho_n(e(r))=\pi_n e(s) \qqq s\,~\text{s.t.}~ \ ns=r\,. \]

• (d) The formula

  (8) \[ \sigma_n: \Q[\Q/\Z] {\to}\Q[\Q/\Z],~ \sigma_n(e(r))= e(nr) \qqq r\in \Q/\Z\,,\ n\in\N \]

  defines an endomorphism of $\Q[\Q/\Z]$ and one has

  (9) \[ \sigma_n \rho_n (x) = x , \]

  (10) \[ \rho_n \sigma_n (x) = \pi_n x. \]

Proof. (a) follows from the divisibility of the group $\Gamma$, which implies the surjectivity of the multiplication by $n$.

(b) One checks that $\pi_n^2=\pi_n$ using (2). Given integers $n$ and $m$, with $\ell=(n,m)$ their gcd, the map $(s,t)\in \Gamma_n\times \Gamma_m\mapsto s+t\in \Gamma_k$ is an $\ell$ to $1$ map onto $\Gamma_k$, where $k=nm/\ell$ is the least common multiple of $n$ and $m$. Thus $\pi_n\pi_m=\pi_k$.

(c) First, the homomorphism $\rho_n$ is well defined since $$ \pi_n e(s)=\frac 1n\sum_{nu=s} e(u) $$ is independent of the choice of $s$ such that $ns=r$. It defines an algebra homomorphism, since with $ns_j=r_j$ one has $$ \rho_n(e(r_1+r_2))=\pi_n e(s_1+s_2)=\pi_n e(s_1)\pi_n e(s_2)=\rho_n(e(r_1))\rho_n(e(r_2)). $$

We then show that $\rho_n$ is an isomorphism with the reduced algebra. We let $\hat\Gamma$ be the (Pontrjagin) dual of $\Gamma$, i.e. the group of characters of the group $\Gamma$. We let $E_n$ be the open and closed subset of $\hat\Gamma$ given by the condition $\chi\in E_n$ if and only if $\chi(\pi_n)=1$. This holds if and only if $\chi|_{\Gamma_n}=1$. This allows one to identify the closed subset $E_n\subset \hat\Gamma$ with the space of characters of the quotient group $\Gamma/\Gamma_n$. Using the identification of $\Gamma/\Gamma_n$ with $\Gamma$ determined by the isomorphism (4), one gets an isomorphism of $E_n \subset \hat\Gamma$ with $\hat\Gamma$, given by

(11) \[ E_n\stackrel{\rho_n^*}{\to}\hat\Gamma,\qquad\chi\mapsto \rho_n^*(\chi),\qquad\rho_n^*(\chi)(r)=\chi(s)\qqq s\,~\text{s.t.}~ \ ns=r. \]

In other words, $\rho_n^*(\chi)=\chi\circ\rho_n$ at the level of the group ring. The range of the algebra homomorphism $\rho_n$ is contained in the reduced algebra by $\pi_n$, and $\rho_n(f)=0$ implies $\langle \rho_n^*(\chi),f\rangle=0$ for all $\chi \in E_n$. It then follows that $f=0$ since $\rho_n^*$ is surjective, hence $\rho_n$ is injective.

To show that the algebra homomorphism $\rho_n$ is surjective on the reduced algebra by $\pi_n$, it is enough to show that the range contains the $\pi_ne(a)$ for all $a\in \Q/\Z$. This follows from (6).

(d) The map $r\in \Q/\Z\mapsto nr \in \Q/\Z$ is a group homomorphism. One has $\sigma_n(\pi_n)=1$ by (5) and one gets (9) using (6). One checks (10) on the generators $e(s)$ using (6). □

2.2 The endomorphisms $\rho_n$ from algebraic geometry

Let us first recall the geometric construction introduced in [4] which gives rise to interesting examples of algebraic endomotives. One lets $(Y,y_0)$ be a pointed smooth algebraic variety (over a field $\K$ of characteristic zero) and $S$ an abelian semi-group of algebraic self-maps $s:Y\to Y$ with $s(y_0)=y_0$, which are finite (of finite degree) and unramified over $y_0$. In this way one then obtains:

$\bullet$ A projective system of algebraic varieties

\[ X_s=\{y\in Y\,|\,s(y)=y_0\}\,, \ \ \xi_{s,s'}: X_{s'} \to X_s \ \ \ \ \xi_{s,s'}(y)=r(y)~\text{if}~s'=rs. \]

$\bullet$ Algebraic morphisms

(12) \[ \beta_s: X=\varprojlim X_u \to X^{e_s}\,, \ \ \xi_u\beta_s(x)=s\xi_u(x) \]

where $X^{e_s}=\xi_s^{-1}(y_0)\subset X$ are open and closed subsets of $X$.

In other words, one obtains in this way a first action $\sigma_s$ of the semigroup $S$ on the projective limit $X=\varprojlim X_u$, since the maps $\beta_s$ given by applying $s$ componentwise commute with the connecting maps of the projective system,

(13) \[ \sigma_s(f)=f\circ \beta_s. \]

In fact, since the maps $\beta_s$ are isomorphisms of $X$ with $X^{e_s}$, it is possible to invert them and define a second action of $S$ that corresponds, at the algebraic level, to the endomorphisms

(14) \[ \rho_s(f)(x) = \begin{cases} f(\beta_s^{-1}(x))&\text{if}~x\in X^{e_s}\\ 0 &\text{if}~x\notin X^{e_s}.\end{cases} \]

The BC-endomotive is a special case of this general construction. It corresponds to the action of the semigroup $S=\N$ by finite algebraic endomorphisms, unramified over $1$, on the pointed algebraic variety $({\Gm}_{/\Q},1)$ (cf. [4, Proposition 3.7]). One has ${\Gm}_{/\Q}=\rm{Spec}(\Q[T^{\pm 1}])$ and the action of $\N$ is given by $a\mapsto a^n$ on the coordinate $a\in \bar \Q$ of the point associated to the character $P(T)\mapsto P(a)$. Equivalently, at the algebra level, this action is described by

(15) \[ \Q[T^{\pm 1}] \ni P(T,T^{-1})\mapsto P(T^n,T^{-n}) \in \Q[T^{\pm 1}]. \]

The point $1\in {\Gm}_{/\Q}$ is a fixed point and its inverse image under the algebraic map $a\mapsto a^n$ is $X_n = \rm{Spec}(\Q[T^{\pm 1}]/(T^n-1))$. The spaces $X_n$ form a projective system indexed by $\N$, with partial order given by divisibility. That is, for a pair of natural numbers $r,n$ with $r = ns$, we have maps

\[ \xi_{n,r}: X_{r} \to X_n,\quad x\mapsto x^s \,. \]

One lets $X=\varprojlim_n X_n$. The base point $1$ belongs to $X_n$ for all $n$ and defines a component $Z_n=\{1\}$ of $X_n$. One checks that the description of the algebra morphisms $\rho_n$ given by (14) agrees with that given in (6). Here the closed and open subset $X^{e_n}\subset X$ of $X$ is simply the inverse image $\xi_{n}^{-1}(Z_n)\subset X$ of $Z_n$ by the canonical map $\xi_{n}$ from the projective limit $X=\varprojlim_n X_n$ to $X_n$.

The relation between this geometric description of the BC-endomotive and the previous group theoretic one can be seen in the following way.

Let $u(n)$ be the class of $T$ mod. $T^n-1$, i.e. the canonical generator of the algebra $\Q[T^{\pm 1}]/(T^n-1))$. Then the homomorphism $\xi_{m,n}$ is given by

(16) \[ \xi_{m,n}(u(n))=u(m)^a\,, \ \ a=m/n\,. \]

The isomorphism with the group theoretic description is then obtained by mapping $u(n) \mapsto e(\frac 1n)\in \Q[\Q/\Z]$.

3. $\F_{1^\infty}$ and the abelian part of the BC-system

In this section we describe the group ring part of the algebra of the BC-system in terms of schemes of finite type over $\F_1$ in the sense of [16]. This is done by introducing a family of affine algebraic varieties $\mu^{(n)}$ over $\F_1$. We will show that these spaces can be organized in two ways: as an inductive system related to the affine multiplicative group scheme over $\F_1$ and also as a pro-variety $\mu^{(\infty)} =\varprojlim_n \mu^{(n)}$. The relation with the BC-system arises exactly when one works with the second system.

We first recall the examples of extensions $\F_{1^n}$ of $\F_1$, developed in [11] and [16], which are the analogues for $q=1$ of the field extensions $\F_{q^n}$ of $\F_q$. The main idea is that these extensions are described by the formula (1) after extending the coefficients from $\F_1$ to $\Z$. Notice that neither $\F_1$ nor its extensions $\F_{1^n}$ need to be properly defined for (1) to make sense. Following [11], while “vector spaces over $\F_1$" correspond to sets, those defined over the extension $\F_{1^n}$ correspond to sets with a free action of the group $\Z/n\Z$.

When $n|m$, one expects in analogy with the case of $\F_{q^n}$ ($q>1$ a rational prime power) to have extensions

(17) \[ \F_{1^n}\subset \F_{1^m}\, \]

(cf. [11], (1.3)). In terms of free actions of roots of unity on sets, and for $m=na$, the functor of restriction of scalars for the extension (17) is obtained by viewing $\Z/n\Z$ as the subgroup of $ \Z/m\Z$ generated by $a$, which is in agreement with (16).

Note also that there is no analogue for $q=1$ of the classification of finite extensions of $\F_q$ for $q$ a prime power, and it is unjustified to consider the inductive limit $\F_{1^\infty}=\varinjlim \F_{1^n}$ of the extensions (17) as the algebraic closure of $\F_1$.

3.1 Affine varieties over $\F_1$

We start by recalling briefly the notion of an affine variety over $\F_1$ as introduced in [16]. Starting with the category of (commutative) rings $R$ with unit, which are finite and flat over $\Z$, we denote by $\cR$ the full sub-category generated by the rings $A_n=\Z[T]/(T^n-1)$ as in (1) and their tensor products (as $\Z$-modules). A gadget $X= (\underline X,\cA_X,e_X)$ over $\F_1$ is specified (cf. [16, Definition 3, §3.4]) by giving the following data:

(a) A covariant functor $\underline X: \cR\to \mathcal Sets$ to the category of sets.

(b) A $\C$-algebra $\cA_X$.

(c) A natural transformation $e_X$ from the functor $\underline X$ to the functor $R\mapsto \Hom(\cA_X,R_\C)$.

The notion of morphism of gadgets is that of natural transformation i.e. a morphism $\phi$ from $X$ to $Y$ is given by a pair $\phi=(\underline \phi, \phi^*)$

(18) \[ \underline \phi: \underline X\to \underline Y\,, \ \ \phi^*: \cA_Y\to \cA_X \]

where $\underline \phi$ is a natural transformation of functors and $\phi^*$ a morphism of algebras. One requires the compatibility with the evaluation maps i.e. one has a commutative diagram

\[ \begin{array}{c c c} \underline X(R) & \underrightarrow{\underline \phi(R)} & \underline Y(R) \\ \downarrow_{e_X(R)} & & \downarrow^{e_Y(R)} \\ \Hom(\cA_X,R_\C) & \underrightarrow{\phi^*} & \Hom(\cA_Y,R_\C) \end{array} \]

A morphism $\phi$ from $X$ to $Y$ is an immersion when $\phi^*$ is injective and for any object $R$ of $\cR$, the map $ \underline \phi(R): \underline X(R)\to \underline Y(R) $ is injective.

The construction described in Section 3.3 of [16] gives a natural covariant functor $\truc$ from the category of varieties over $\Z$ (i.e. schemes of finite type over $\Z$) to the category $\cT$ of gadgets over $\F_1$. More precisely

Lemma 3.1 An affine variety $V$ over ${\mathbb Z}$ defines a gadget $X=\cF(V)$ over ${\mathbb F}_1$ by letting

(19) \[ \underline X(R)={\rm Hom}_\Z(\cO(V),R)\,, \ \ \cA_X=\cO(V)\otimes_\Z \C, \ \ e_X(f)=f\otimes id_\C, \forall f\in \underline X(R)\,. \]

One then defines (cf. [16, Definition 3])

Definition 3.2 An affine variety over $\F_1$ is a gadget $X$ such that:

$\bullet$ $X(R)$ is finite for any object $R$ of $\cR$.

$\bullet$ There exists an affine variety $X_{\mathbb Z}$ over ${\mathbb Z}$ and an immersion $i : X \rightarrow \cF(X_{\mathbb Z})$ of gadgets satisfying the following property: for any affine variety $V$ over ${\mathbb Z}$ and any morphism of gadgets $ \varphi : X \rightarrow \cF(V)\, , $ there exists a unique algebraic morphism $$ \varphi_{\mathbb Z} : X_{\mathbb Z} \rightarrow\textbf{} V $$ such that $\varphi = \cF(\varphi_{\mathbb Z}) \circ i$.

3.2 The varieties $\mu^{(k)}$

We introduce the varieties $\mu^{(k)}$ over $\F_1$, as examples of affine varieties over $\F_1$. We begin by defining the associated functors ${\underline \mu}^{(k)}: \cR \to \mathcal Sets$. These are given (for $k\in \N$) by the assignments

(20) \[ {\underline \mu}^{(k)}(R)=\{x\in R\,|\,x^k=1\}, \]

i.e. ${\underline \mu}^{(k)}$ is the functor represented by the ring $A_k$

(21) \[ {\underline \mu}^{(k)}(R)={\rm Hom}_\Z(A_k,R)\qqq R\in \mathcal Obj(\cR)\,. \]

Notice that the functors ${\underline \mu}^{(k)}$ can be organized in two different ways:

• a) As an inductive system converging to ${\underline \mu} = \underline{\Gm}$, where ${\Gm}(R):=\mu(R)$ is the multiplicative group $\Gm$ over $\F_1$, as affine variety over $\F_1$ (cf. [16, 5.2.2]).
• b) As a projective system converging to ${\underline \mu}^{(\infty)}$, where ${\underline \mu}^{(\infty)}(R):= \varprojlim_k{\rm Hom}(A_k,R) = {\rm Hom}(\Z[\Q/\Z],R)$.

For a), one uses the natural inclusion

(22) \[ {\underline \mu}^{(n)}(R)\subset {\underline \mu}^{(m)}(R)\quad \forall~n|m \]

which corresponds at the level of the rings $A_n$ representing these functors, to the surjective ring homomorphism

(23) \[ A_m\twoheadrightarrow A_n=A_m/(T^n-1)\quad \forall~n|m. \]

Then, the union of the ${\underline \mu}^{(k)}(R)$ is simply the functor ${\underline \mu}(R)$ which assigns to $R\in \mathcal Obj(\cR)$ the set of all roots of $1$ in $R$. In the formalism of [16] this functor is part (a) of the data (a)-(c) for the multiplicative group $\mu={\Gm}$ as an affine variety over $\F_1$.

To explain b), we use the homomorphisms (16). These homomorphisms organize the ${\underline \mu}^{(k)}(R)$ into a projective system. The connecting maps are given by raising a root of $1$ to the power $a=m/n$. Then, the elements of ${\underline \mu}^{(\infty)}(R)$ are described by homomorphisms of the group $\Q/\Z$ to the multiplicative group of $R$. The equality ${\underline \mu}^{(\infty)}(R)={\rm Hom}(\Z[\Q/\Z],R)$ follows from (21).

After tensoring by $\Z$ as in (1), the scalars extensions $\F_{1^n}\subset \F_{1^m}$ of (17) (cf. [11], (1.3)) correspond to homomorphisms of rings

(24) \[ \xi_{m,n}: \F_{1^n}\otimes_{\F_1}\Z\to \F_{1^m}\otimes_{\F_1}\Z\, \]

given by

(25) \[ \xi_{m,n}(u(n))=u(m)^a\,, \ \ a=m/n\,, \]

where $u(n)$ is the canonical generator $T\in A_n$. These agree with the maps (16) that define the integral version of the abelian part of the BC-system.

In order to complete the definition of the varieties $\mu^{(n)}$ over $\F_1$, we use the functor $\cF$ of Lemma 3.1. In other words we define

(26) \[ \mu^{(n)}=\truc \Sp(A_n). \]

One checks (cf. [16, §4, Proposition 2]) that it fulfills the conditions of Definition 3.2. We then obtain the following result.

Proposition 3.3 The $\mu^{(n)}$ defined as in (26) form a projective system of zero-dimensional affine varieties over $\F_1$.

Proof. It follows from (21) that the corresponding functors ${\underline \mu}^{(k)}$ are the same as the ones defined by (20). The morphisms (16) turn the varieties $\Sp(A_n)$ into a projective system and thus, since $\truc$ is a covariant functor, we get that the $\mu^{(n)}$ form a projective system of varieties over $\F_1$. □

4. The integral BC-endomotive

Having to work over $\Z$ creates a problem when one implements the semigroup action via the maps $\rho_n$, which involve denominators, as in (6) and (5). However, as shown in the algebro-geometric description of the BC-algebra ( Proposition 2.1, (d)), the partial inverses of the $\rho_n$, which we have denoted by $\sigma_n$, do not involve denominators, therefore we will be able to consider them over $\Z$.

The partial inverse relations between the $\sigma_n$ and $\rho_n$ are given by (9) and (10).

Since by (21) the schemes $\underline{\mu}^{(n)}$ are represented by the rings $A_n$, by Yoneda's lemma the ring homomorphisms $\sigma_n$ given by

(27) \[ \sigma_n: A_k \to A_k\, \ \ \ \ u(k)\mapsto u(k)^n \]

define (contravariantly) morphisms of schemes. These induce morphisms of the pro-scheme $\underline{\mu}^{(\infty)}$ by the compatibility

(28) \[ \xi_{\ell,k}\circ \sigma_n=\sigma_n\circ \xi_{\ell,k} \qqq k|\ell \qqq n\in \N. \]

In Proposition 6.1 we will show how the maps $\sigma_n$ in fact give rise to endomorphisms of the varieties $\mu^{(k)}$ over $\F_1$.

In the limit, the endomorphisms $\sigma_n$ are surjective

(29) \[ \sigma_n\,:\, \varinjlim_k A_k \twoheadrightarrow \varinjlim_k A_k . \]

In fact, in the group ring notation of Section 2.1, one gets $\sigma_n(e(r))=e(nr)$, while one has the surjectivity of multiplication by $n$ in the exact sequence (4). However, the $\sigma_n$ are not the same as the endomorphisms $\rho_n$, since the latter are injective and describe ring isomorphisms between reduced algebras and the projectors $\pi_n$, as we have shown in Proposition 2.1.

The kernel of $\sigma_n$ in (29) is the ideal $J_n$ generated by the element $u(n)-1$, or in group-ring notation by $e(1/n)-1$. This means that $\sigma_n^{-1}(f)$ is only defined modulo $J_n$. If one allows inverting $n$, then there is a natural complementary subspace to $J_n$, namely the reduced algebra by the projection $\pi_n$. However, when we work over $\Z$ (and a fortiori over $\F_1$) we cannot invert $n$, and we need to adapt the presentation of the BC-endomotive. The data of the BC-endomotive, i.e. the abelian algebra and the endomorphisms, combine to produce a noncommutative crossed product algebra with a natural time evolution defined over $\C$. This quantum statistical mechanical system is the BC-system which we recall below.

4.1 $C^*$-algebra description of the BC-system

At the $C^*$-algebra level the BC system is given by $1_{\hat \Z}(C_0(\A_{\Q,f})\rtimes \Q_+^*)1_{\hat \Z}$, namely by the algebra of the crossed product $C_0(\A_{\Q,f})\rtimes \Q_+^*$ reduced by the projection $1_{\hat \Z}\in C_0(\A_{\Q,f})$. Here $\A_{\Q,f}$ denotes the locally compact space of finite adeles of $\Q$ and $\hat \Z\subset \A_{\Q,f}$ the open compact subset closure of $\Z$. The reduced algebra can be described as the convolution algebra of the locally compact étale groupoid $\cG$ obtained as the reduction of the groupoid $\A_{\Q,f}\rtimes \Q_+^*$ by the open and closed set of units $\hat \Z\subset \A_{\Q,f}$. Concretely, the groupoid $\cG$ is the étale groupoid of pairs

(30) \[ \cG=\{ (r,\rho)\, | \, r\in \Q^*_+,\, \rho\in \hat\Z, \, \text{ such that } r\rho\in \hat\Z \}, \]

with source and range maps $(r,\rho)\mapsto \rho$ and $(r,\rho)\mapsto r\rho$, and composition

(31) \[ (r_1,\rho_1)\circ (r_2,\rho_2)=(r_1 r_2,\rho_2), \ \ \ \text{ if } r_2\rho_2=\rho_1. \]

The $C^*$-algebra $C^*(\cG)$ of a locally compact étale groupoid $\cG$ is obtained as the completion of the algebra $C_c(\cG)$ of compactly supported functions on $\cG$ with the convolution product

(32) \[ f_1*f_2(g)=\sum_{g_1g_2=g} f_1(g_1)f_2(g_2), \]

the involution

(33) \[ f^*(g)=\overline{f(g^{-1})} \]

and the norm

(34) \[ \| f \|:= \sup_{y\in \cG^{(0)}} \| \pi_y (f)\|_{\cB(\cH_y)}. \]

Here every unit $y\in \cG^{(0)}$ defines a representation $\pi_y$ by left convolution of the algebra $C_c(\cG)$ on the Hilbert space $\cH_y=\ell^2(\cG_y)$, where $\cG_y$ denotes the set of elements in $\cG$ with source $y$. Namely, one has

(35) \[ (\pi_y(f)\xi)(g) = \sum_{g_1g_2=g} f(g_1)\xi(g_2). \]

The $C^*$-algebra $C^*(\cG)$ contains $C(\hat \Z)$ as a subalgebra and is generated by $C(\hat \Z)$ and the elements $\mu_n$ given by the compactly supported functions

(36) \[ \mu_n(n,\rho)=1\qqq \rho\in \hat\Z\,, \ \ \mu_n(r,\rho)=0 \qqq r\neq n\,, \rho\in \hat\Z\,. \]

One identifies the Pontrjagin dual of the group $\Q/\Z$ with the compact group $\hat\Z= \Hom(\Q/\Z,\Q/\Z)$ using the pairing $$\langle \gamma,\rho\rangle= e^{2\pi i \rho(\gamma)}\qqq \gamma \in \Q/\Z\,, \ \rho \in \Hom(\Q/\Z,\Q/\Z) $$ and one lets $e(\gamma)\in C^*(\cG)$ be given by the function

(37) \[ e(\gamma)(r,\rho)=0 \qqq r\neq 1\,,\ \ e(\gamma)(1,\rho)=\langle \gamma,\rho\rangle\,. \]

The time evolution is given by the following one-parameter group of automorphisms of the $C^*$-algebra $C^*(\cG)$:

(38) \[ \sigma_t (\mu_n) = n^{it} \mu_n , \ \ \sigma_t (\mu_n^*) = n^{-it} \mu_n^* , \ \ \ \ \ \sigma_t (e(\gamma))=e(\gamma). \]

Definition 4.1 The BC-system is the complex dynamical system defined by the pair $(C^*(\cG),\sigma_t)$.

We refer to [6, Chapter 3, §4] for the equivalent descriptions of the $C^*$-algebra of the BC-system and of the relation with $\Q$-lattices. Working over $\C$ one considers the subalgebra of $C^*(\cG)$ generated by the characters $e(\gamma)$, $\gamma\in \Q/\Z$ the $\mu_n$ and their adjoints $\mu_n^*$. We shall now explain the presentation of this algebra over $\Q$.

4.2 The BC-algebra over $\Q$

We first recall the presentation of the crossed product algebra $\cA_\Q=\Q[\Q/\Z]\rtimes \N$ of the BC system in characteristic zero.

The group ring $\Q[\Q/\Z]$ has the canonical additive basis $e(\gamma)$, $\gamma\in\Q/\Z$, with $e(\gamma)^* = e(-\gamma)$ and $e(\gamma_1+\gamma_2) = e(\gamma_1)e(\gamma_2)$. To obtain the crossed product, one considers then generators $\mu_n$ and $\mu_n^*$, $n\in\N$, which satisfy the following conditions:

(c1) $\mu_n^*\mu_n = 1\,, \ \ \forall~n$

(c2) $\mu_{nm} = \mu_n\mu_m\,, \ \mu^*_{nm} = \mu^*_n\mu^*_m\,, \ \ \forall~n,m$,

(c3) $\mu_n\mu_m^* = \mu_m^*\mu_n\,, \ \ \text{if}~ (m,n)=1$

together with the additional relation

(c4) $\mu_n e(\gamma)\mu_n^* = \frac{1}{n}\sum_{n\delta = \gamma}e(\delta)\,, \ \ \forall n,~\gamma$.

In particular, the relation (c4) can be interpreted algebraically by means of the homomorphism $\rho_n(x)$ (cf. (6)) projecting onto the reduced algebra by the idempotent $\pi_n$. This means

(c4') $\rho_n(x) = \mu_n x\mu_n^*\,, \ \ \forall~x\in\Q[\Q/\Z]$.

As a consequence of (c1) and (c4') we get

\[ (\mu_n\mu_n^*)^2=(\mu_n\mu_n^*)(\mu_n\mu_n^*) = \mu_n\mu_n^* = \rho_n(1) = \frac{1}{n}\sum_{n\gamma=0}e(\gamma) \]

In this way we get a description of the projector $\pi_n\in\Q[\Q/\Z]$ as in (5) by means of the new generators of the crossed product i.e. $\pi_n=\rho_n(1)=\mu_n\mu_n^*$. It also follows from (c1) that $\mu_n\mu_n^*\mu_n = \mu_n$. Since the surjective endomorphisms $\sigma_n$ are partial inverses of $\rho_n$, that is

\[ \sigma_n\rho_n(e(\gamma)) = \frac{1}{n}\sum_{n\gamma'=\gamma}\sigma_n(e(\gamma')) = \frac{1}{n}\sum_{n\gamma'=\gamma}e(n\gamma') = e(\gamma), \]

one gets $\sigma_n\rho_n(x) = x$, $\forall~x\in\Q[\Q/\Z]$.

We then have the following easy consequence

Proposition 4.2 The following relations hold in the algebra $\cA_\Q=\Q[\Q/\Z]\rtimes_\rho\N$:

(39) \[ \mu_n x = \rho_n(x) \mu_n, \ \ \ \ \forall x \in \Q[\Q/\Z], \, \forall n \in \N, \]

(40) \[ \mu_n^* x = \sigma_n(x) \mu_n^*, \ \ \ \ \forall x \in \Q[\Q/\Z], \, \forall n \in \N, \]

(41) \[ x \mu_n = \mu_n \sigma_n(x), \ \ \ \ \forall x \in \Q[\Q/\Z], \, \forall n \in \N. \]

Proof. Relation (39) follows from

(42) \[ \mu_n x \mu_n^* = \rho_n(x) \]

and the fact that $\mu_n^* \mu_n =1$. For (40), we use the idempotent $\pi_n=\mu_n\mu_n^*=\rho_n(1)$. We first assume that $x =\pi_n x$ belongs to the reduced algebra by $\pi_n$. It then follows that $x= \rho_n(y)$ for some $y\in \Q[\Q/\Z]$ (hence $y=\sigma_n(x)$). By applying (c4') and (c1), this shows that

\[ \mu_n^* x= \mu_n^* \rho_n(y) = \mu_n^* \mu_n y \mu_n^*= y \mu_n^* =\sigma_n(x) \mu_n^*. \]

In the general case, we notice that in view on (c1), the left hand side of (40) does not change by replacing $x$ by $\mu_n\mu_n^* x= \pi_n x$. The right hand side does not change either, since $\sigma_n (\pi_n) =1$, hence (40) holds with no restriction. The relation (40) also gives

(43) \[ \mu_n^*x\mu_n = \sigma_n(x) \]

by multiplying on the right by $\mu_n$ and applying (c1). The relation (41) then follows by (43) together with $x\mu_n = \pi_n x \mu_n = x \pi_n \mu_n$. □

Remark 4.3 Notice that the involution (33) of the $C^*$-algebra $C^*(\cG)$ restricts to an involution of the rational algebra $\cA_\Q=\Q[\Q/\Z]\rtimes \N$ with the properties

(44) \[ e(\gamma)\mapsto e(-\gamma)\,, \ \ \mu_n\mapsto \mu_n^*\,, \ \ \mu_n^*\mapsto \mu_n\,. \]

Note that the full presentation of the rational algebra involves the two relations that appear in (c2). In particular this is needed for the involution (44) to make sense.

4.3 The maps $\tilde\rho_n$

When one wants to generalize the definition of the algebra $\cA_\Q=\Q[\Q/\Z]\rtimes_\rho\N$ to the case where the field of coefficients is a perfect field $\K$ of positive characteristic (for example $\K = \F_p$), as well as in extending the original (rational) formulation of the algebra to the case of integer coefficients, one is faced with the problem of “dividing by $n$" in the definition of the endomorphisms $\rho_n$ (e.g. when $\K=\F_p$, for $n=p$). However, up to multiplying the original definition of the maps $\rho_n$ by $n$, the linear maps

(45) \[ \tilde\rho_n: \K[\Q/\Z] \to \K[\Q/\Z]\,, \ \ \tilde\rho_n(e(\gamma))= \sum_{n\gamma'=\gamma}e(\gamma') \]

retain a meaning (when $\text{char}(\K)=p>0$ and $n=p$ and also over $\Z$), since $e(\gamma)$ is a linear basis of the algebra $\K[\Q/\Z]$ as a $\K$-vector space. In particular, when $\text{char}(\K)=p>0$, the operator $\tilde{\pi}_p = \tilde\rho_p(1) = \sum_{p\gamma=0}e(\gamma) \neq 0$ is nilpotent since

\[ \tilde{\pi}_p^2 = (\sum_{p\gamma=0}e(\gamma))(\sum_{p\gamma'=0}e(\gamma'))=\sum_{\gamma,\gamma'}e(\gamma+\gamma') = p\sum_{p\gamma”=0}e(\gamma”) = 0. \]

Compare this with the idempotents $\pi_n$ of (5). Moreover, over a perfect field of characteristic $p>0$ one gets $\sigma_p\tilde\rho_p = 0$, since $\sigma_p\tilde{\pi}_p = \sigma_p\tilde\rho_p(1) = \sigma_p\sum_{p\gamma=0}e(\gamma) = \sum_{p\gamma=0}e(p\gamma) = 0$. This means that $\text{Range}(\tilde\rho_p)\subset\text{Ker}(\sigma_p)$.

Proposition 4.4 When working over $\Z$ the $\sigma_n$ continue to make sense and define endomorphisms of $\Z[\Q/\Z]$ which fulfill the following relations with the maps $\tilde\rho_m$:

(46) \[ \sigma_{nm}=\sigma_{n}\sigma_{m}\,,\ \ \tilde\rho_{mn}=\tilde\rho_{m}\tilde\rho_{n}\qqq m,n \]

(47) \[ \tilde\rho_{m}(\sigma_m(x)y)=x\tilde\rho_{m}(y)\qqq x,y\in \Z[\Q/\Z] \]

(48) \[ \sigma_c(\tilde\rho_b(x))=(b,c)\,\tilde\rho_{b'}(\sigma_{c'}(x))\,, \ \ b'=b/(b,c)\,, \ \ c'=c/(b,c)\,, \]

where $(b,c)$ denotes the gcd of $b$ and $c$.

Proof. One has by definition $\sigma_n(e(\gamma))=e(n\gamma)$, which shows that $\sigma_n$ is an endomorphism of $\Z[\Q/\Z]$ and $\sigma_{nm}=\sigma_{n}\sigma_{m}$. To get $\tilde\rho_{mn}=\tilde\rho_{m}\tilde\rho_{n}$ we let, for $x\in \Q/\Z$ and $n\in \N$,

(49) \[ E_n(x)=\{y\in \Q/\Z\,|\, ny=x\}\,. \]

One has $$ E_{nm}(x)=\cup_{y\in E_n(x)}E_m(y)\,, \ \ y_1\neq y_2\Rightarrow E_m(y_1)\cap E_m(y_2)=\emptyset $$ thus $$ \tilde\rho_{m}(\tilde\rho_{n}(e(x)))=\tilde\rho_{m}(\sum_{E_n(x)}e(y))=\sum_{y\in E_n(x)}\sum_{z\in E_m(y)}e(z)=\tilde\rho_{mn}(e(x))\,. $$ To check (47) we can assume that $x=e(s)$, $y=e(t)$ with $s,t\in \Q/\Z$. One has $\sigma_m(x)y=e(ms)e(t)=e(ms+t)$. For $u\in \Q/\Z$, one has $mu=ms+t$ iff $u-s\in E_m(t)$ thus $E_m(ms+t)=s+E_m(t)$ which proves (47).

To check (48) we assume that $x=e(s)$ and let $n=(b,c)$ so that $b=nb'$, $c=nc'$ with $(b',c')=1$. One has $$ E_b(s)=\{u\in \Q/\Z\,|\, bu=s\}=\{u\in \Q/\Z\,|\, nb'u=s\} $$ Thus the multiplication by $c=nc'$ is an $n$ to $1$ map from $E_b(s)$ to $E_{b'}(c's)$. This proves (48). □

In particular one gets:

Corollary 4.5 The range of $\tilde\rho_{m}$ is an ideal in $\Z[\Q/\Z]$. When $n$ and $m$ are relatively prime $\sigma_n$ commutes with $\tilde\rho_{m}$.

Proof. The range of $\tilde\rho_{m}$ is additive by construction and is invariant under multiplication by $\Z[\Q/\Z]$ using (47). The second statement follows from (48). □

Remark 4.6 Notice that, although the $\tilde \rho_n$ are not ring homomorphisms, the relation (47) which they fulfill suggests the existence of an associated correspondence (in the form of a bimodule). This would fit with a more general framework for the theory of endomotives that uses correspondences instead of endomorphisms as in [14].

4.4 The BC-algebra over $\Z$

When $\K$ denotes either $\Z$ or a perfect field of positive characteristic, the relations (40) continue to make sense, because the $\sigma_n$ are well defined. On the other hand, the relation (39) involves the $\rho_n$ which are not well defined. However, in the case of integral coefficients and in characteristic $p$, the linear maps $\tilde\rho_n$ of (45) make sense and in the latter case these maps play the role of the $p\rho_p$. Thus, in order to extend the relation (39), we keep the generators $\mu_n^*$ and introduce new generators $\tilde\mu_n$ (in place of the $\mu_n$'s), which play the role, in characteristic $p$, of the operators $p\mu_p$ and in general fulfill the relation

(50) \[ \tilde\mu_n x \mu_n^* = \tilde\rho_n(x), \]

that is the analog of (42). These relations reformulate (c4') in the case of integral coefficients and make sense in positive characteristic.

Definition 4.7 The algebra $\cA_\Z=\Z[\Q/\Z]\rtimes_{\tilde\rho}\N$ is the algebra generated by the group ring $\Z[\Q/\Z]$, and by the elements $\tilde\mu_n$ and $\mu_n^*$, with $n\in\N$, which satisfy the relations:

(51) \[ \begin{array}{l} \tilde\mu_n x \mu_n^* = \tilde\rho_n(x)\ \ \ \ \\ \mu_n^* x = \sigma_n(x) \mu_n^* \\ x \tilde\mu_n = \tilde\mu_n \sigma_n(x), \end{array} \]

where $\tilde\rho_m$, $m\in\N$ is defined in (45), as well as the relations

(52) \[ \begin{array}{l} \tilde\mu_{nm}= \tilde\mu_n \tilde\mu_m \qqq n,m\\ \mu_{nm}^* =\mu_{n}^*\mu_{m}^* \qqq n,m\\ \mu_n^* \tilde\mu_n =n \\ \tilde\mu_n\mu_m^* = \mu_m^*\tilde\mu_n \ \ \ \ (n,m) = 1. \end{array} \]

Our first task is to check that these relations are sufficient to express every element of $\cA_\Z$ as a finite sum of elementary monomials labeled by a pair $(x,r)$ where $x\in \Z[\Q/\Z]$ and $r\in \Q_+^*$ is an irreducible fraction $r=a/b$.

Lemma 4.8 Any element of the algebra $\cA_\Z$ is a finite sum of monomials:

(53) \[ \tilde\mu_a\,x \, \mu^*_b\,, \ \ \ (a,b) = 1\,, \ \ x\in \Z[\Q/\Z]\,, \]

where by convention $\tilde\mu_1=\mu^*_1=1$.

Proof. It is enough to show that the product of monomials of the form (53) is still of the same form. We take a product of the form $$ \tilde\mu_a\,x \, \mu^*_b\,\tilde\mu_c\,y \, \mu^*_d\, $$ Let then $n$ be the gcd of $b=nb'$ and $c=nc'$. One has $$ \mu^*_b\,\tilde\mu_c=\mu^*_{b'}\,\mu^*_n\,\tilde\mu_n\tilde\mu_{c'}=n \mu^*_{b'}\,\tilde\mu_{c'}=n\,\tilde\mu_{c'}\mu^*_{b'} $$ so that $$ \tilde\mu_a\,x \, \mu^*_b\,\tilde\mu_c\,y \, \mu^*_d=n\,\tilde\mu_a\,x \, \tilde\mu_{c'}\mu^*_{b'}\,y \, \mu^*_d=\,n\,\tilde\mu_a\,\tilde\mu_{c'}\sigma_{c'}(x)\sigma_{b'}(y) \mu^*_{b'}\, \mu^*_d $$ Let then $m$ be the gcd of $ac'=mu$ and $b'd=mv$. One has $$ \tilde\mu_a\,\tilde\mu_{c'}=\tilde\mu_u\,\tilde\mu_{m}\,, \ \ \mu^*_{b'}\, \mu^*_d=\mu^*_{m}\, \mu^*_v $$ so that: $$ \tilde\mu_a\,x \, \mu^*_b\,\tilde\mu_c\,y \, \mu^*_d=n\,\tilde\mu_u\,\tilde\mu_{m}\,\sigma_{c'}(x)\sigma_{b'}(y)\,\mu^*_{m}\, \mu^*_v= n\,\tilde\mu_u\, \tilde\rho_m(\sigma_{c'}(x)\sigma_{b'}(y))\,\mu^*_v\,. $$ Since $u$ and $v$ are relatively prime and $z=\tilde\rho_m(\sigma_{c'}(x)\sigma_{b'}(y))\in \Z[\Q/\Z]$ it follows that the product of two monomials of the form (53) is still a monomial of the same form. Note also that

(54) \[ u/v=(a/b)(c/d) \]

since $u/v=ac'/(b'd)=ac/(bd)$. Thus the labels $a/b\in \Q_+^*$ are multiplicative. □

Remark 4.9 Using the surjectivity of the endomorphisms $\sigma_n$ one can rewrite the monomials (53) in the form $y\,\tilde\mu_a\, \mu^*_b$, $\tilde\mu_a\, \mu^*_b\, z$ or $\mu^*_b\, t\, \tilde\mu_a$. The reason for choosing (53) is that, in this form, there is no ambiguity in the choice of $x$ while the lack of injectivity of $\sigma_a$ and $\sigma_b$ introduces an ambiguity in the choices of $y$, $z$ and $t$. At the geometric level this corresponds, using (36), to the fact that the initial support of $\tilde\mu_a$ is $1$.

In order to check that the relations of Definition 4.7 are coherent we shall now construct a faithful representation of these relations (which is the left regular representation of $\cA_\Z$) in the free abelian group $\cE=\Z[\Q/\Z\times \Q_+^*]$. We denote by $\xi(x,r)$ the element of $\cE$ associated to $x\in \Z[\Q/\Z]$ and $r\in \Q_+^*$.

Proposition 4.10 The following relations define a faithful representation of the algebra $\cA_\Z$ on $\cE$,

(55) \[ x \,\xi(y,c/d)=\xi(\sigma_c(x)y,c/d)\qqq c,d\,, \ (c,d)=1 \]

(56) \[ \tilde\mu_a\,\xi(y,c/d)= \xi(\tilde\rho_m(y),ac/d)\,, \ \ m=(a,d) \]

(57) \[ \mu_b^*\,\xi(y,c/d)=(b,c)\, \xi(\sigma_{b/n}(y),c/bd)\,, \ \ n=(b,c)\,. \]

Proof. We shall check that the relations of Definition 4.7 are fulfilled. The relation (55) shows that the left action of $\Z[\Q/\Z]$ is a representation which is a direct sum of copies of the left regular representation of $\Z[\Q/\Z]$ composed with the $\sigma_c$.

Using the notation $(a,b)$ for ${\rm gcd}(a,b)$ one has the equality

(58) \[ (a_1a_2,d)=(a_1,d)(a_2,d/(a_1,d)) \]

and the fact that the left action of $\tilde\mu_a$ fulfills $\tilde\mu_{a_2a_1}=\tilde\mu_{a_2}\tilde\mu_{a_1}$ follows from (46) which gives $$ \tilde\rho_m(y)=\tilde\rho_{m_2}(\tilde\rho_{m_1}(y))\,, \ m_1=(a_1,d)\,, \ m_2=(a_2,d/(a_1,d))\,, \ m=(a_1a_2,d)\,. $$ In order to check the relation $x \tilde\mu_a = \tilde\mu_a \sigma_a(x)$ one uses (47). One has $$ x \tilde\mu_a\,\xi(y,c/d)=x \,\xi(\tilde\rho_m(y),ac/d)=\xi(\sigma_k(x)\tilde\rho_m(y),ac/d)\,, \ k=ac/m\,, \ m=(a,d) $$ $$ \tilde\mu_a \sigma_a(x)\,\xi(y,c/d)=\tilde\mu_a \xi(\sigma_c(\sigma_a(x))y,c/d)= \xi(\tilde\rho_m(\sigma_{ac}(x)y),ac/d) $$ and since $ac=mk$, (47) gives $$ \tilde\rho_m(\sigma_{ac}(x)y)=\sigma_k(x)\tilde\rho_m(y)\,. $$ Let us check the relation $\mu^*_{b_2b_1}=\mu^*_{b_2}\mu^*_{b_1}$. Let $n_1=(b_1,c)$ and $b'_1=b_1/n_1$, $c'_1=c/n_1$ then $$ \mu_{b_1}^*\,\xi(y,c/d)=n_1\,\xi(\sigma_{b'_1}(y),c'_1/(b'_1d)) $$ so that, with $n_2=(b_2,c'_1)$ and $b'_2=b_2/n_2$, $c'_2=c'_1/n_2$ one gets $$ \mu_{b_2}^*(\mu_{b_1}^*\,\xi(y,c/d))=n_2n_1\, \xi(\sigma_{b'_2}\sigma_{b'_1}(y),c'_2/(b'_2b'_1d))\,. $$ By (58) one has $n_1n_2=(b_1,c)(b_2,c/n_1)=(b_1b_2,c)=n$ and with $b=b_1b_2$ one has $$b'=b/n=(b_1/n_1)(b_2/n_2)=b'_1b'_2$$ $$c'_2=c'_1/n_2=c/(n_1n_2)=c/n=c'$$ This shows, using $\sigma_{ab}=\sigma_a\sigma_b$, that $$ \mu_{b_2}^*(\mu_{b_1}^*\,\xi(y,c/d))=\mu_{b_2b_1}^*\,\xi(y,c/d)\,. $$ Let us now check the relation $\mu_b^* x = \sigma_b(x) \mu_b^* $. One has, with $n=(b,c)$, $b'=b/n$, $c'=c/n$, $$ \mu_b^*( x\,\xi(y,c/d))=\mu_b^*\,\xi(\sigma_c(x)y,c/d)=n\,\xi(\sigma_{b'}(\sigma_c(x)y),c/bd) $$ $$ \sigma_b(x)(\mu_b^*\,\xi(y,c/d))=n\,\sigma_b(x)\xi(\sigma_{b'}(y),c'/b'd)=n\, \xi( \sigma_{c'}(\sigma_b(x))\,\sigma_{b'}(y),c/bd) $$ Thus the relation follows from the multiplicativity of $\sigma_{b'}$ and the equality $b'c=c'b$.

Let us check the relation $\tilde\mu_b x \mu_b^* = \tilde\rho_b(x)$. One has $$ x (\mu_b^*(\xi(y,c/d)))=n\, \xi(\sigma_{c'}(x) \sigma_{b'}(y),c'/{b'd})\,, \ \ n=(b,c)\,, \ b'=b/n\,, \ c'=c/n\,. $$ To multiply by $\tilde\mu_b$ on the left, one uses (56) and gets $$ \tilde\mu_b(x (\mu_b^*(\xi(y,c/d))))=n\,\xi( \tilde\rho_m(\sigma_{c'}(x) \sigma_{b'}(y)),u/v) $$ where $m=(b,b'd)$ and $u=bc'/m$, $v=b'd/m$. One has $m=b'$ since it divides $b=n b'$ and $b'd$ while $bc'/b'=c$ is prime to $d$. Thus $u=c$ and $v=d$ and one gets $$ \tilde\mu_b(x (\mu_b^*(\xi(y,c/d))))=n\,\xi( \tilde\rho_{b'}(\sigma_{c'}(x) \sigma_{b'}(y)),c/d)\,. $$ In particular it is divisible by $n$ and one needs to understand why the other side, namely $\tilde\rho_b(x)\xi(y,c/d)$ is also divisible by $n=(b,c)$. This follows from (48) since, $$ \tilde\rho_b(x)\xi(y,c/d)=\xi(\sigma_c(\tilde\rho_b(x))y,c/d) $$ (by (55)) while by (48), $$ \sigma_c(\tilde\rho_b(x))=(b,c)\,\tilde\rho_{b'}(\sigma_{c'}(x))\,, \ \ b'=b/(b,c)\,, \ \ c'=c/(b,c)\,. $$ One then uses (47) to obtain $$ \tilde\rho_{b'}(\sigma_{c'}(x) \sigma_{b'}(y))=\tilde\rho_{b'}(\sigma_{c'}(x))\,y $$ which gives the required equality.

Let us now check the relation $\mu_a^*\tilde\mu_a=a$. By (56) one has $$ \tilde\mu_a\,\xi(y,c/d)= \xi(\tilde\rho_m(y),u/v) $$ where $m=(a,d)$ is the gcd of $ac=mu$ and $d=mv$. We then get with $a=ma'$, $d=md'$ that $u=a'c$ and $v=d'$. The left action of $\mu_a^*$ is given by $$ \mu_a^*(\tilde\mu_a\,\xi(y,c/d))=\mu_a^*\xi(\tilde\rho_m(y),u/v)=n\,\xi( \sigma_{a”}(\tilde\rho_m(y)),c”/(a”d')) $$ where $n=(a,a'c)$, $c”=a'c/n$, $a”=a/n$. One has $n=a'$ since $(m,c)=1$ as $m=(a,d)$ is a divisor of $d$ and $(c,d)=1$. It follows that $c”=a'c/n=c$, $a”=a/n=m$. Thus by (48) $\sigma_{a”}(\tilde\rho_m(y))=my$. Also $a”d'=md'=d$, thus $$ n\,\xi( \sigma_{a”}(\tilde\rho_m(y)),c”/(a”d'))=nm\,\xi(y,c/d) $$ and the required equality follows from $nm=a$.

It remains to check that $\tilde\mu_a\mu_b^* = \mu_b^*\tilde\mu_a$ when $(a,b) = 1$. Let, as above, $m=(a,d)$ and write $a=ma'$, $d=md'$ so that $u=a'c$ is prime to $v=d'$. One has $$ \mu_b^*(\tilde\mu_a\,\xi(y,c/d))=\mu_b^*\,\xi(\tilde\rho_m(y),u/v)=n\,\xi( \sigma_{b/n}(\tilde\rho_m(y)),ac/(bd)) $$ where $n=(b,u)$. Since $(a,b)=1$ one has $(a',b)=1$ and $n=(b,u)=(b,a'c)=(b,c)$. Thus by (57), $$ \mu_b^*\,\xi(y,c/d)=n\,\xi(\sigma_{b/n}(y),c/bd) $$ When applying $\tilde\mu_a$ on the left, one uses (56). One lets $m=(a,b'd)$ where $b'=b/n$ so that $b'd$ is the reduced denominator of $c/bd$. By (56), one has $$ \tilde\mu_a\,\mu_b^*\,\xi(y,c/d)=n\,\tilde\mu_a\,\xi(\sigma_{b/n}(y),c/bd)= n\,\xi(\tilde\rho_m(\sigma_{b/n}(y)),ac/bd) $$ Since $(a,b)=1$ one has $m=(a,b'd)=(a,d)$ and the required equality follows from the second statement of Corollary 5.5 since $m$ and $b/n$ are relatively prime so that $\sigma_{b/n}$ and $\tilde\rho_m$ commute. We have shown that the relations of Definition 4.7 are fulfilled. One has, for $(a,b)=1$,

(59) \[ \tilde\mu_a\,x\,\mu_b^*\,\xi(1,1)=\xi(x,a/b) \]

which shows that the map $x\in \cA_\Z\mapsto x\,\xi(1,1)\in \cE$ is an isomorphism of abelian groups, and hence the representation of $\cA_\Z$ in $\cE$ is faithful. □

Corollary 4.11 The monomials

(60) \[ \tilde\mu_a\,e(r) \, \mu^*_b\,, \ \ \ (a,b) = 1\,, \ \ r\in \Q/\Z \,, \]

form a basis of $\cA_\Z$ as a free abelian group.

Proof. By construction $\cE=\Z[\Q/\Z\times \Q_+^*]$ is a free abelian group with basis the $\xi(e(r),a/b)$ for $r\in \Q/\Z$ and $a/b\in \Q_+^*$. Moreover by (59) and Proposition 4.10 the map $x\in \cA_\Z\mapsto x\,\xi(1,1)\in \cE$ is an isomorphism of abelian groups.□

While Proposition 4.10 describes the left regular representation of the algebra $\cA_\Z$, Proposition 4.4 allows one to construct a representation of $\cA_\Z$ on its abelian part $\Z[\Q/\Z]$ as follows.

Proposition 4.12 The relations

(61) \[ \begin{array}{l} \theta(x)\,\xi=x\xi \qqq x,\xi \in \Z[\Q/\Z] \\ \theta(\tilde\mu_n)\xi=\tilde\rho_n(\xi)\qqq \xi \in \Z[\Q/\Z],\forall n \\ \theta(\mu_n^*) \xi =\sigma_n(\xi)\qqq \xi \in \Z[\Q/\Z],\forall n \end{array} \]

define a representation $\theta$ of $\cA_\Z$ on $\Z[\Q/\Z]$.

Proof. It is enough to check that the relations of Definition 4.7 are fulfilled. The first of the three relations (51) follows from (47). The second follows from the multiplicativity of $\sigma_n$. The third one follows again from (47). The first two of the four relations (52) follow from the analogous relation (46) on the $\tilde\rho_n$ and $\sigma_n$. The last two relations both follow from (48).□

4.5 Relation with the integral Hecke algebra

The original construction of the BC-system [1] is based on Hecke algebras of quasi-normal pairs. One considers the inclusion $P_\Z^+ \subset P_\Q^+$ where the “$ax+b$” algebraic group $P$ is viewed as the functor which to any abelian ring $R$ assigns the group $P_R$ of 2 by 2 matrices over $R$ of the form

(62) \[ P_R = \left\{ \left( \begin{matrix} 1 &b \\ 0 &a \end{matrix} \right) \, ; \ a,b \in R \, , \ a \ \hbox{invertible} \right\} \, . \]

Here $\Gamma_0=P_\Z^+$ and $\Gamma=P_\Q^+$ denote the restrictions to $a>0$. This inclusion $\Gamma_0\subset\Gamma$ is such that the orbits of the left action of $\Gamma_0$ on $\Gamma / \Gamma_0$ are all finite. The same clearly holds for orbits of $\Gamma_0$ acting on the right on $\Gamma_0 \backslash \Gamma$.

The integral Hecke algebra ${\mathcal H}_\Z (\Gamma, \Gamma_0)$ is by definition the convolution algebra of functions of finite support

(63) \[ f : \Gamma_0 \backslash \Gamma \to \Z , \]

which fulfill the $\Gamma_0$-invariance condition

(64) \[ f (\gamma \gamma_0) = f(\gamma), \ \ \ \ \forall \gamma \in \Gamma, \forall \gamma_0 \in \Gamma_0, \]

so that $f$ is defined on $\Gamma_0 \backslash \Gamma / \Gamma_0$. The convolution product is then defined by the formula

(65) \[ (f_1 * f_2)(\gamma) = \sum_{\Gamma_0 \backslash \Gamma} f_1 (\gamma \gamma_1^{-1}) f_2 (\gamma_1) \, . \]

There is a presentation of this algebra which is obtained as an extension of the integral group ring $\Z[\Q/\Z]$ by adjoining elements $\nu_n$ and $\nu_n^*$ which are formally defined by $\nu_n=\sqrt n \mu_n$, $\nu^*_n=\sqrt n \mu^*_n$ (with the notations of [1 §4], i.e. $\mu_n = n^{-1/2}e_{X_n}$). The presentation is of the form:

(66) \[ \begin{array}{l} \nu_n x \nu_n^* = \tilde\rho_n(x)\ \ \ \ \\ \nu_n^* x = \sigma_n(x) \nu_n^* \,, \ x \nu_n = \nu_n \sigma_n(x), \\ \nu_{nm}= \nu_n \nu_m \,, \ \nu_{nm}^* =\nu_{n}^*\nu_{m}^* \qqq n,m\\ \nu_n^* \nu_n =n \,, \ \nu_n\nu_m^* = \nu_m^* \nu_n \ \ \ \ (n,m) = 1. \end{array} \]

Comparing this presentation with (51) and (52) one obtains:

Proposition 4.13 There exists a unique isomorphism

(67) \[ \phi: ~{\mathcal H}_\Z (\Gamma, \Gamma_0)\stackrel{\sim}{\longrightarrow} \cA_\Z=\Z[\Q/\Z]\rtimes_{\tilde\rho}\N,\notag \] \[ \phi(e(r))=e(r)\qqq r\in \Q/\Z\,, \ \ \phi(\nu_n)=\tilde\mu_n\,, \ \ \phi(\nu^*_n)=\mu_n^*\,. \]

Proof. One checks that the relations (66) transform into (51) and (52) under $\phi$. □

The Hecke algebra ${\mathcal H}_\Z (\Gamma, \Gamma_0)$ admits a natural involution for which $\nu_n$ and $\nu_n^*$ are adjoint of each other. It is given (with arbitrary coefficients) by:

(68) \[ f^* (\gamma) := \overline{f(\gamma^{-1})}, \ \ \ \forall \gamma \in \Gamma_0 \backslash \Gamma / \Gamma_0. \]

The rational algebra $\cA_\Z\otimes\Q=\cA_\Q=\Q[\Q/\Z]\rtimes_{\rho}\N$ also admits a natural involution which coincides with (68) on the subalgebra $\Z[\Q/\Z]$ and whose extension to $\cA_\Z$ is dictated by the equation $\tilde\mu_n=n(\mu_n^*)^*$.

Notice that the isomorphism $\phi$ of Proposition 4.13 does not preserve the involution. The rational subalgebras ${\mathcal H}_\Q (\Gamma, \Gamma_0)$ and $\cA_\Z\otimes_\Z\Q=\cA_\Q$ of the $C^*$-dynamical system $(C^*(\cG),\sigma_t)$ of Definition 4.1 are not the same. One has however

Proposition 4.14 The involutive algebras $\cA_\Z\otimes_\Z\Q=\Q[\Q/\Z]\rtimes_{\tilde\rho}\N$ and ${\mathcal H}_\Q (\Gamma, \Gamma_0)$ become isomorphic after tensoring by $\C$. An isomorphism is given by

(69) \[ \psi(e(r))=e(r)\qqq r\in \Q/\Z\,, \ \ \psi(\nu_n)=n^{-1/2}\,\tilde\mu_n\,, \ \ \psi(\nu^*_n)=n^{1/2}\,\mu_n^*\,. \]

The corresponding rational subalgebras of the $C^*$-dynamical system $(C^*(\cG),\sigma_t)$ are conjugate under $\sigma_{i/2}$.

Proof. As subalgebras of the $C^*$-algebra $C^*(\cG)$, the above involutive $\Q$-algebras are generated by the $e(r)$ and respectively by the $\mu_n$ and $\mu_n^*$ for $\cA_\Z\otimes_\Z\Q$ and by the $\nu_n=n^{1/2}\mu_n$ and $\nu_n^*=n^{1/2}\,\mu_n^*$ for ${\mathcal H}_\Q (\Gamma, \Gamma_0)$. Thus they are the same after tensoring with $\C$. To get the conjugacy by $\sigma_{i/2}$, note that one has $\sigma_t(\mu_n)=n^{it}\mu_n$ and $\sigma_t(\mu_n^*)=n^{-it}\mu_n^*$. Thus with $\tilde\mu_n=n\mu_n$ one gets $\sigma_{i/2}(\tilde\mu_n)=n^{1/2}\mu_n=\nu_n$ and $\sigma_{i/2}(\mu_n^*)=n^{1/2}\mu_n^*=\nu^*_n$. □

Remark 4.15 The above distinction between the two rational subalgebras of Proposition 4.14 is overlooked in Proposition 3.25 of [6, Chapter III]. However by Proposition 4.14 , these two rational algebras are conjugate by $\sigma_{i/2}$ and the $\sigma_t$ invariance of KMS$_\beta$ states thus shows that the values of the restriction of KMS$_\beta$ states is independent of this distinction.

5. The endomotive and algebra in characteristic $p$

The group ring $\Z[\Q/\Z]$ together with the endomorphisms $\sigma_n$ and the maps $\tilde\rho_n$ give a model over $\Z$ of the BC-endomotive.

In this section we study the reduction of this model at a prime $p$ both at the level of the endomotive and of the noncommutative crossed product algebra. From now and throughout this section we shall work over a perfect field $\K$ of characteristic $p>0$, such as a finite extension $\F_q$ of $\F_p$ or a separable closure of $\F_p$.

We first show that, by applying reduction at $p$ and specializing $n$ to be $p^\ell$, the endomorphism $\sigma_n$ on $\K[\Q/\Z]$ is identified with the geometric Frobenius correspondence. The group algebra $\K[\Q/\Z]$ decomposes as a tensor product of the group algebra $\K[\Q_p/\Z_p]$ of the $p$-torsion $\Q_p/\Z_p$ of $\Q/\Z$ by the group algebra of fractions with denominators prime to $p$. The structure of the latter algebra is essentially insensitive to characteristic $p$. The new fact specific to characteristic $p$ is that the group algebra $\K[\Q_p/\Z_p]$ is unreduced and in fact local. We concentrate on this “$p$-part" of the abelian algebra.

We then form a new noncommutative algebra obtained as the crossed product of the $p$-part $\K[\Q_p/\Z_p]$ by the sub-semigroup of $\N$ given by powers of $p$. We exhibit the nilpotent nature of this algebra by showing that it admits a faithful representation as infinite triangular matrices.

5.1 The endomotive in characteristic $p$

The relevant properties of the algebra $\cA_\Z(\K)$ can be isolated by decomposing the groups as follows

(70) \[ \Q/\Z=\Q_p/\Z_p\times (\Q/\Z)^{(p)} \,. \]

Here $\Q_p/\Z_p$ is identified with the subgroup of $\Q/\Z$ of fractions with denominator a power of $p$ and $(\Q/\Z)^{(p)}$ is interpreted as the subgroup of $\Q/\Z$ of fractions with denominator prime to $p$. At the group algebra level one gets

(71) \[ \K[\Q/\Z]=\K[\Q_p/\Z_p]\otimes \K[(\Q/\Z)^{(p)}]\,. \]

The decomposition

(72) \[ \Q_+^*=p^{\Z}\times \Q_+^{(p)} \]

corresponds to the decomposition of the semigroup $\N$ as a product of the semigroup $p^{\Z^+}$ of powers of $p$ and the semigroup $\N^{(p)}$ of numbers prime to $p$. There is no essential difference with the characteristic zero set-up for the action of $\N^{(p)}$ on $\K[\Q/\Z]$. In fact, the endomorphism $\rho_n$ on $\K[\Q/\Z]$ retains a meaning when $n$ is prime to $p$, since the denominators in the definition of the projection $\pi_n$ and of $\rho_n$ (i.e. the partial inverse of $\sigma_n$) are integers prime to p. Moreover, we notice that when $n$ is prime to $p$ the equation $T^n-1=0$ is unramified. On the other hand, when $n\in p^{\Z^+}$ there is no way to single out the component of $\{1\}$ in $\Sp(A_n)$ since in that case the above equation has $1$ as a multiple root. Therefore, our study will focus on the understanding of

$\bullet$ The endomorphism $\sigma_n$, for $n=p^\ell\in p^{\Z^+}$

$\bullet$ The algebra $A_{p^\infty}=\varinjlim_\ell A_{p^\ell}\otimes_\Z \K=\K[\Q_p/\Z_p]$

We first show the relation between the endomorphisms $\sigma_n$, for $n=p^\ell\in p^{\Z^+}$, and the (relative) geometric Frobenius homomorphism acting on the algebra $A_{p^\infty}$.

Proposition 5.1 Let $\sigma_{\F_p}\in \Aut( \K)$ be the small Frobenius automorphism given by $\sigma_{\F_p}(x)=x^p$ for all $x\in \K$, then for any $\ell$,

(73) \[ (\sigma_{p^\ell}\otimes \sigma_{\F_p}^\ell)(f)=f^{p^\ell}\qqq f\in \K[\Q/\Z]=\Z[\Q/\Z]\otimes_\Z \K,\,\ \ \ \forall \ell\in\N. \]

Proof. Both sides of (73) define an endomorphism of the ring, thus it is enough to check that they agree on elements of the form $e(r)\otimes x$, for $x\in\K$ and $r\in \Q/\Z$. One has $$ (\sigma_{p^\ell}\otimes \sigma_{\F_p}^\ell)(e(r)\otimes x)=e(p^\ell r)\otimes x^{p^\ell}=(e(r)\otimes x)^{p^\ell}\,, $$ which gives the required equality. □

Remark 5.2 The relation $(\sigma_{p^\ell}\otimes \sigma_{\F_p}^\ell)(f)=f^{p^\ell}$ of (73) shows that we can interpret $\sigma_{p^\ell}$ as the Frobenius correspondence acting on the pro-variety $(\mu^{(\infty)}\otimes_\Z \K)$. This means that at the fixed level $\mu^{(m)} = \text{Spec}(A_{m})$, the definition of $\sigma_{p^\ell}$ coincides with the Frobenius morphism $\varphi$ as in [17], p. 24 (i.e. the morphism inducing in étale cohomology the geometric Frobenius $\Phi$ of Deligne).

An equivalent description of the algebra $A_{p^\infty}=\varinjlim_\ell A_{p^\ell}\otimes_\Z \K=\K[\Q_p/\Z_p]$ will be given in terms of the following (local) convolution algebra of functions which displays an explicit choice of a basis. At a fixed level $\ell$, i.e. for the algebra $A_{p^\ell}$, this choice of basis corresponds to the powers $\epsilon^k$ of the natural generator $\epsilon= \delta_{p^{-\ell}}$, as in (75), of the maximal ideal of the local ring $A_{p^\ell}$, cf.  Remark 5.9.

Definition 5.3 We define the algebra $\cT(p)$ (over $\K$) as the convolution algebra of $\K$-valued functions with finite support on the semigroup $S_+=\cup \frac{1}{p^n}\Z^+\subset \R$, modulo the ideal of functions with support in $S\cap [1,\infty[$, with the convolution product given by

(74) \[ f_1\star f_2(c)=\sum_{a+b=c}f_1(a)f_2(b). \]

We extend any function $f$ on $S_+$ to a function on $S=\cup \frac{1}{p^n}\Z$ which fulfills $f(a)=0$ for all $a<0$. This extension is compatible with the convolution product. By construction the algebra $\cT(p)$ is commutative and local. It has a unique character: the homomorphism of $\K$-algebras given by evaluation at $0$, that is,

\[ \epsilon_0: \cT(p)\to \K\,, \ \ f\mapsto f(0). \]

Any element in the kernel of this character is nilpotent. The kernel $\text{Ker}(\epsilon_0)$ of this character is the only maximal ideal.

For any $a\in S\cap [0,1)$ we let $\delta_a\in \cT(p)$ be given by

(75) \[ \delta_a(a)=1\,, \ \ \delta_a(b)=0 \ \text{if} \ b\neq a\,. \]

Any $f\in \cT(p)$ is a finite sum $f=\sum f(a) \delta_a$ and $\delta_0$ is the unit ${\bf 1}$ of the algebra $\cT(p)$.

Proposition 5.4 1) The following map induces in the limit an isomorphism of $A_{p^\infty}$ with $\cT(p)$,

(76) \[ \iota\;:\; A_{p^\ell}\otimes_\Z \K\to \cT(p)\,, \ \ \iota(e(1/p^\ell))= {\bf 1}-\delta_{p^{-\ell}}. \]

2) The endomorphism $\sigma_p$ corresponds by the above isomorphism to the following endomorphism of $\cT(p)$,

(77) \[ \sigma_p(f)(a)=f(a/p)\qqq f\in \cT(p). \]

3) The map $\tilde\rho_p$ corresponds by the above isomorphism to the following map of $\cT(p)$,

(78) \[ \tilde\rho_p(f)(a)=f(p\,a-(p-1))\qqq f\in \cT(p). \]

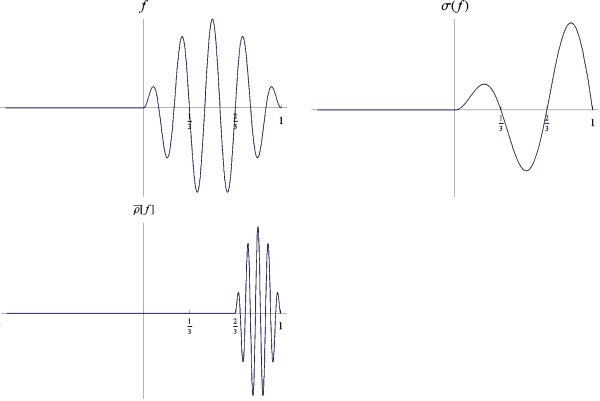
Fig. 1: The maps $\sigma_p$ and $\tilde\rho_p$

Note that both maps $\sigma_p$ and $\rho_p$ are given by an affine change of variables as shown in Fig. 1

Proof. 1) Let us check that the $\iota(e(1/p^\ell))$ fulfill the rules of the generators $e(1/p^\ell)$. In characteristic $p$ one has $$ ({\bf 1}-T)^{p^\ell}={\bf 1}-T^{p^\ell} $$ Thus to show that $\iota(e(1/p^\ell))^{p^\ell}={\bf 1}$ it is enough to check that the $p^\ell$ power of the characteristic function $\delta_{p^{-\ell}}$ is equal to $0$. This follows from the equalities $\delta_a\star \delta_b=\delta_{a+b}$ (using (74)) and $\delta_1=0$. In fact one needs to show that $$\iota(e(1/p^\ell))^p=\iota(e(1/p^{\ell-1}))$$ which means that $$ ({\bf 1}-\delta_{p^{-\ell}})^p={\bf 1}-\delta_{p^{-\ell+1}} $$ and this follows from $\delta_{p^{-\ell}}^p=\delta_{p^{-\ell+1}}$.

2) It is enough to check (77) on the elements $\iota(e(1/p^\ell))={\bf 1}-\delta_{p^{-\ell}}=\delta_0-\delta_{p^{-\ell}}$. The right hand-side of (77) defines an endomorphism of $\cT(p)$ which transforms $\delta_a$ into $\delta_{pa}$ and this gives $\sigma_p(e(1/p^\ell))=e(1/p^{\ell-1})$ as required.

3) Note that since $f$ is extended to a function on $S=\cup \frac{1}{p^n}\Z$ which fulfills $f(a)=0$ for all $a<0$, the formula (78) makes sense and the function $\rho_p(f)$ vanishes on the interval $[0,\frac{p-1}{p})$. In characteristic $p$ one has, with $q=p^\ell$,

(79) \[ \sum_0^{q-1}\, T^k=({\bf 1}-T)^{q-1} \]

since multiplying both sides by $({\bf 1}-T)$ gives $({\bf 1}-T)^{q}$. This shows that

(80) \[ \iota(\tilde\rho_p(1))=\sum_0^{p-1}\iota(e(k/p))=({\bf 1}-\iota(e(1/p))^{p-1}=\delta_{\frac{p-1}{p}}\,. \]

Now, by (47), one has $$ \tilde\rho_p(\sigma_p(x))=x \tilde\rho_p(1)\qqq x\in A_{p^\infty} $$ which gives the required equality (78) using the surjectivity of $\sigma_p$ and the fact that in the algebra $\cT(p)$ the convolution by $\iota(\tilde\rho_p(1))=\delta_{\frac{p-1}{p}}$ is given by the translation by $\frac{p-1}{p}$. □

Corollary 5.5 The kernel of $\sigma_p$ is the nilpotent ideal

(81) \[ \ker\, \sigma_p=\{f \in \cT(p)\,|\, f(a)=0\qqq a\in [0,\frac 1p)\} \]

Proof. One has $f\in \ker\, \sigma_p$ iff $f(a/p)=0$ for all $a\in S\cap [0,1)$ which gives (81). Any element $f\in \ker\, \sigma_p$ thus fulfills $f^p=0$ in the algebra $\cT(p)$. □

5.2 The BC-algebra in characteristic $p$

By definition, the BC-algebra over $\K$ is the tensor product:

(82) \[ \cA_\Z(\K)=\cA_\Z\otimes_\Z\K \]

By Corollary 4.11 the $\K$-linear space $\cA_\Z(\K)$ coincides with the vector space $\K[\Q/\Z\times \Q_+^*]$ and because of that we will work with the corresponding linear basis of monomials (60).

The remaining part of this section is dedicated to the study of the algebra

(83) \[ \cC_p= A_{p^\infty}\rtimes_{\tilde\rho}p^\N \sim \cT(p)\rtimes_{\tilde\rho}p^\N \]

We shall refer to $\cC_p$ as to the $p$-part of the algebra $\cA_\Z(\K)$. We keep the same notation as in Section 4.4.

Lemma 5.6 The following monomials form a linear basis of the algebra $\cC_p$:

(84) \[ \tilde\mu_p^n\,\delta_a \,, \ n\in \N\,, \ a\in S\cap [0,1) \,, \ \ \delta_a {\mu_p^*}^m \,, \ m\geq 0\,, \ a\in S\cap [0,1)\,. \]

Proof. For $m=0$ we use the notation ${\mu_p^*}^0=1$ so that the above monomials contain the algebra $A_{p^\infty}$ and the generators $\tilde\mu_p$ and $\mu_p^*$. Thus it is enough to show that the linear span of these monomials is stable under the product. One has

(85) \[ \tilde\mu_p^n\,x\,\tilde\mu_p^m\,y=\tilde\mu_p^{n+m}\sigma_p^m(x)y\,,\ \ \ x {\mu_p^*}^n\,y {\mu_p^*}^m=x\sigma_p^n(y){\mu_p^*}^{n+m} \]

and, for $n>0$,

(86) \[ x{\mu_p^*}^n\,\tilde\mu_p^m\,y=0 \]

while

(87) \[ \tilde\mu_p^n\,x\,y {\mu_p^*}^m=\begin{cases} \tilde\rho_p^n(xy){\mu_p^*}^{m-n}&\text{if}~m\geq n\\ \tilde\mu_p^{n-m}\tilde\rho_p^m(xy) &\text{if}~n>m.\end{cases} \]

which shows that the linear span of the above monomials is an algebra. □

Note that Lemma 5.6 also follows directly from Lemma 4.8.

In order to exhibit the nilpotent nature of this algebra we now show that the representation of Proposition 4.12 is given by infinite triangular matrices.

We let $\K[S\cap[0,1)]$ be the $\K$-linear space of $\K$-valued functions with finite support on $S\cap[0,1)$ and denote by $\xi_a$, $a\in S\cap[0,1)$ its canonical basis. For $a\in S_+, a\geq 1$ we let $\xi_a=0$ by convention.

Let $G=S\rtimes \Z$ be the semi-direct product of the additive group $S$ by the action of $\Z$ whose generator acts on $S$ by multiplication by $p$. The group $G$ acts on $S$ by affine transformations

(88) \[ \alpha_{g}(b)=p^n b+ a\qqq g=(n,a)\in G\,, \ b\in S\,. \]

Lemma 5.7 Let $G$ be the group defined above.

• The condition

  (89) \[ x\geq a\Rightarrow g(x)\geq a\qqq a\in [0,1] \]

  defines a sub-semigroup $G^+\subset G$.

• $G^+$ acts on $\K[S\cap[0,1)]$ by

  \[ \tau(g)\xi_a=\xi_{g(a)}. \]

• The semi-group $G^+$ is generated by the elements $g_a=(0,a)$, for $a\in S\cap[0,1)$, $\alpha=(-1, (p-1)/p)$, $\beta=(1,0)$.

Proof. The first statement is obvious. The second follows from (89) for $a=1$. Let us prove (3). Let $g=(n,a)\in G^+$. If $n=0$ then $g=g_a$ with $a\geq 0$. If $n>0$ then $g(x)=p^nx+a$ and taking $x=0$ shows that $a\geq 0$ so that $g=g_a\beta^n$. For $n=-m<0$, $g(x)=p^{-m}x+a$. Taking $x=1$ and using (89), one gets $p^{-m}+a\geq 1$ i.e. $a=1-p^{-m}+b$ for some $b\geq 0$. Thus $g=g_b\alpha^m$.□

Proposition 5.8 The equations

(90) \[ \begin{array}{l} \theta(\delta_b)\,\xi_a=\tau(g_b)\xi_a=\xi_{a+b}\ \ \ \ \\ \theta(\tilde\mu_p)\, \xi_a= \tau(\alpha)\xi_a= \xi_{\frac{a+p-1}{p}}, \\ \theta(\mu_p^*)\, \xi_a =\tau(\beta)\xi_a=\xi_{pa} \end{array} \]

define a faithful representation

\[ \cC_p \stackrel{\theta}{\to} \text{End}(\K[S\cap[0,1)]) \]

of the algebra $\cC_p$ by (lower)-triangular matrices $T=(T_{a,b})$, $T_{a,b}\in \K$ with $a,b\in S\cap[0,1)$.

Proof. The matrix associated to $T\in \text{End}(\K[S\cap[0,1)])$ is defined by

(91) \[ (Tf)(a)=\sum T_{a,b}\, f(b)\qqq f\in \K[S\cap[0,1)] \]

Thus the matrices associated to the operators given in (90) are:

(92) \[ \begin{array}{l} (\delta_a)_{c,d}=0\,\ \text{if}\ c-d\neq a \,,\ \ (\delta_a)_{c,c-a}=1 \\ (\tilde\mu_p)_{c,d}=0\,\ \text{if}\ c\neq \frac{d+p-1}{p}\,,\ \ (\tilde\mu_p)_{c,d}=1\,\ \text{if}\ c= \frac{d+p-1}{p} \\ (\mu_p^*)_{c,d}=0\,\ \text{if}\ c\neq pd\,, \ (\mu_p^*)_{c,c/p}=1\,. \end{array} \]

They are lower triangular. Indeed one has $$ c\geq c-a\,, \ \ \frac{d+p-1}{p}>d\,, \ \ p\,d\geq d \qqq c,d\in S\cap[0,1)\,. $$ One then needs to show that the defining relations of the algebra $\cC_p$ are fulfilled. These relations are obtained from the presentation of Definition 4.7 by restriction to the $p$-part. Thus they are fulfilled by specializing Proposition 4.12 to the $p$-part. One can also check them directly. By construction the action of the $\delta_a$ gives a representation of the convolution algebra $\cT(p)$. The three relations of (51)

(93) \[ \begin{array}{l} \tilde\mu_p\, x \mu_p^* = \tilde\rho_p(x)\ \ \ \ \\ \mu_p^*\, x = \sigma_p(x) \mu_p^* \\ x \tilde\mu_p = \tilde\mu_p \sigma_p(x), \end{array} \]

follow directly from the group action $\tau$. Moreover one has the additional relation $$ \mu_p^*\,\tilde\mu_p\, \xi_a=\mu_p^*\,\xi_{\frac{a+p-1}{p}}=\xi_{ a+p-1 }=0, $$ which corresponds to the third relation of (52). Its validity follows from $\xi_b=0$ for all $b\geq 1$.

Let us prove that the representation is faithful. By Lemma 5.6 any element $x\in\cC_p$ is a finite linear combination $x=\sum \lambda_j \tau(g_j)$ ($\lambda_j\in \K$) of monomials with $g_j\in G^+$. Now for any two distinct elements $g, h\in G^+$ the set of elements $a\in S$ such that $g(a)=h(a)$ contains at most one element. Thus, since $g_j(0)\in [0,1)$, one can find an element $b\in S\cap [0,1)$ such that $$ g_j(b)\in S\cap [0,1)\qqq j \,, \ \ g_j(b)\neq g_k(b)\qqq j\neq k\,. $$ We then have $$ x\,\xi_b=\sum \lambda_j \tau(g_j)\,\xi_b=\sum \lambda_j \xi_{g_j(b)} $$ and $x\xi_b\neq 0$ if $x\neq 0$. Thus the representation is faithful. □

Remark 5.9 By construction the algebra $A_{p^\infty}$ is the inductive limit of the local rings $A_q=\K[T]/(T^q-1)$, $q=p^\ell$. We let

(94) \[ \tilde\pi_q =\tilde\rho_q(1)= 1+T+\cdots +T^{q-1}\in A_q=\Z[T]/(T^q-1). \]

The local ring $\K[T]/(T^q-1)$ is generated over $\K$ by the nilpotent element $\epsilon = T-1$ ($\epsilon^q = 0$). The principal ideal of multiples of $\epsilon$ is the maximal ideal. We use the natural decreasing finite filtration by powers of the maximal ideal,

(95) \[ F^i(\K[T]/(T^q-1))=\epsilon^i\,\K[T]/(T^q-1) \]

One has, using (80),

(96) \[ \tilde\pi_q =\epsilon^{q-1}\in F^{q-1}(\K[T]/(T^q-1))\,, \ \ F^q(\K[T]/(T^q-1))=\{0\} \]

Thus the operator $\tilde\pi_q$ detects the top piece of the filtration.

The following equalities show that the subalgebra $\cP\subset A_{p^\infty}$ generated by the $\tilde\rho_p^m(1)=\tilde \pi_{p^m}=\tau_m$ is stable under the $\tilde\rho_p$ and $\sigma_p$.

(97) \[ \tau_m\tau_n=0\,, \ \ \tilde\rho_p^m(\tau_n)=\tau_{m+n} \,, \ \ \sigma_p(\tau_n)=0 \qqq m,n\in \N\,. \]

As above one checks that the following monomials form a linear basis of the crossed product algebra $\cP\rtimes_{\tilde\rho}p^\N$:

(98) \[ \tilde\mu_p^n\,\tau_k \,, \ n\in \N\,, \ k\geq 0 \,, \ \ \tau_k {\mu_p^*}^m \,, \ m\geq 0\,, \ k\geq 0\,. \]

Since $\cP\rtimes_{\tilde\rho}p^\N$ is a subalgebra of the algebra $\cC_p$, Proposition 5.8 yields in particular, a triangular representation of $\cP\rtimes_{\tilde\rho}p^\N$.

5.3 The effect of reduction

In the original definition of endomotives given in [4], we assumed that the algebras are reduced. This is in agreement with the classical definition of Artin motives (cf. [8, II p. 211]). In the present context, namely working over a perfect field $\K$ of characteristic $p$, one can still restrict to reduced algebras by functorial reduction. One can see in the result below that this reduction introduces a drastic simplification of the algebra, which, in particular, eliminates the problem of denominators.

Proposition 5.10 The reduced algebra of $\varinjlim_n A_n\otimes_\Z \K$ is the group ring over $\K$ of the subgroup of $\Q/\Z$ of fractions with denominator prime to $p$. Moreover, $\sigma_p$ induces an automorphism on the reduced algebra.

Proof. This amounts to showing that for $n=p^km$ with $m$ prime to $p$, the reduced algebra of $\K[T]/(T^n-1)$ is the algebra $\K[T]/(T^m-1)$. If $n=p^km$ then the group $\Z/n\Z$ splits canonically as a product of $\Z/p^k\Z$ and $\Z/m\Z$. At the group ring level, this corresponds to a tensor product decomposition. Since the reduction in characteristic $p$ of the group ring of $\Z/p^k\Z$ is the ground field $\K$, the first factor in the tensor product disappears and the reduction only leaves the second factor. This proves the first statement. It is then enough to observe that, for $m$ prime to $p$, the multiplication by $p$ is an automorphism of $\Z/m\Z$. Since $\sigma_p$ preserves the levels, this is compatible with the map of the inductive system of algebras. □

Corollary 5.11 In the case of the reduced algebra in characteristic $p$, the inverses $\rho_n$ of the $\sigma_n$ only involve denominators that are prime to $p$.

Proof. The case where $n$ is prime to $p$ is clear. Suppose that $n=p^k$. Then by Proposition 5.10 , $\sigma_n$ is an automorphism of the reduced algebra since multiplication by $n$ is an automorphism of the group $(\Q/\Z)^{(p)}$. One then defines $\rho_n$ as its inverse and the corresponding $\pi_n$ is then equal to one, since $\sigma_n$ is injective. □

Note that passing from $\Q/\Z$ to the subgroup $(\Q/\Z)^{(p)}$ (i.e. the prime-to-$p$ component) is the same, when dealing with the Pontrjagin dual groups, as removing from the ring of finite adeles the component at $p$. This suggests that there is a connection with the localized system at $p$ in (cf. [5 Definition 8.14, Theorem 8.15]). Note however that unlike the setting of [5], here the coefficients are taken in a field of positive characteristic, so that the notion of KMS states should be taken in the extended sense of [7].

Remark 5.12 Notice that reducing the abelian part of the algebra and then taking the crossed product as we did in this section is not the same thing as moding out the crossed product algebra $\cA_\Z$ by its nilpotent radical.

5.4 Endomotives in the unreduced case

As we have seen in the previous sections, when taking coefficients in a field of positive characteristic the BC-endomotive involves unreduced finite dimensional commutative algebras which strictly speaking do not correspond to classical Artin motives. The construction in characteristic $p$ that we gave in the case of the BC-algebra in fact extends to a more general class of endomotives constructed from finite, self maps of algebraic varieties as in [4], but without requiring that these maps are unramified over the base point.

This leads us naturally to consider the problem of a general construction of endomotives in arbitrary characteristic. Roughly speaking, an endomotive over a (perfect) field $\K$ is given by assigning:

$\bullet$ An inductive system of augmented commutative $\K$-algebras, finite dimensional as vector spaces over a perfect field $\K$ (i.e. Artinian commutative $\K$-algebras).

$\bullet$ A commutative family of correspondences $\sigma_n$.

This set of data should of course be compatible with the constructions that we have developed in this paper as well as in [4], namely

1) It should determine homomorphisms (correspondences) such as the $\rho_n$'s, when denominators (i.e. division by $n$) are allowed.

2) It should be fulfilled by the endomotives associated to self-maps of pointed varieties as described in [4, Example 3.4].

6. The BC endomotive over $\F_1$

In this section we show that the BC endomotive has a model defined over $\F_1$ from which one recovers the original endomotive by extension of scalars to $\Q$.

Proposition 6.1

• a) The BC-endomotive has a model over $\F_1$.
• b) The original BC-endomotive is obtained by extension of the scalars from $\F_1$ to $\Q$.

Proof. We start with the projective system of affine varieties $\mu^{(n)}$ over $\F_1$, defined as in Section 3 and Proposition 3.3. This system shows that the abelian part of the BC endomotive is defined over $\F_1$. Notice that these are pointed varieties because the algebras $A_n$ are naturally augmented. The augmentations fit together in the inductive system of algebras because they come from the natural augmentation of the group ring.

It remains to show that the $\sigma_n$ are morphisms of varieties over $\F_1$ in the sense of [16]. This is a consequence of the construction of the projective system of the varieties $\mu^{(n)}$ over $\F_1$, as these are obtained by applying the functor $\cF$ from varieties over $\Z$ to gadgets over $\F_1$ (cf.  Proposition 3.3). Notice that the maps $\sigma_n$ preserve levels and are given at each level $A_n$ by (27). Thus, the $\sigma_n$ are morphisms in the category of varieties over $\Z$, and as such they define morphisms of varieties over $\F_1$ through the functor $\cF$. □

Remark 6.2 Proposition 6.1 shows that the BC-endomotive can be defined over $\F_1$, according to the theory developed by C. Soulé in [16]. However, we also want to emphasize that since our proof is mainly based on a description of the BC-algebra which is obtained using the family of algebraic endomorphisms σn $\sigma_n$ ($n\in \N$) of the affine group-variety $\Gm$ (cf. Section 2.2), it continues to hold— independently of the detailed theory of varieties over $\F_1$ as in op. cit.—as long as one is able to show that the space $\Gm$ and the endomorphisms σn are defined over $\F_1$. The forthcoming paper [3] will introduce and develop a theory of geometric spaces over $\F_1$ which is a refinement of the one contained in [16]. In the case of $\Gm$, the two theories agree and determine the same space over $\F_1$. The advantage of the construction in [3] is that of being properly linked to the geometric theory developed by J. Tits [18], in relation to the study of semi-simple algebraic groups.

6.1 The automorphisms of $\F_{1^\infty}/\F_1$ and the symmetries of the BC system

In [10], the analog of the Frobenius automorphism for the extension $\F_{1^\infty}$ of $\F_1$ is described as follows. Suppose given a set $X$ with a free action of the roots of unity (that is a vector space over $\F_{1^\infty}$ when one adds an extra fixed point $0$). Then, given an element $\alpha \in \hat\Z^*$ (and more in general a non-invertible one in $\hat\Z$) one defines a new action on the same set by the rule

(99) \[ \zeta: x \mapsto \zeta^\alpha x. \]

For $\alpha = n$ an integer, this means that one replaces the action of a root of unity $\zeta$ by that of $\zeta^n$. The $\hat\Z$-powers of the Frobenius are then defined by setting

(100) \[ \psi^\alpha:\F_{1^\infty} \to \F_{1^\infty} \]

to be the map that sends the action of roots of unity $\zeta$ on a given $\F_{1^\infty}$-vector space $X$ to the action by $\zeta^\alpha$.

When reformulated additively, after making an identification of the group of roots of unity with $\Q/\Z$, one can write the action (99) in the form

(101) \[ e(r) \mapsto e(\alpha(r)), \]

where $\alpha\in\hat\Z$ is seen as an element in $\hat\Z=\Hom(\Q/\Z,\Q/\Z)$.

Thus, in terms of the BC system, the Frobenius appears naturally in the semigroup action. This is the case of (101) where $n$ is an integer and it gives the action of the $\sigma_n$. Moreover, it is also important to keep in mind that the Frobenius action (101) also recovers the symmetries of the BC system. In fact, the symmetries by automorphisms, given by $\hat\Z^*$ act exactly like the corresponding Frobenius $\psi^{\hat\Z^*}$ (cf. [1], [4]).

6.2 The Frobenius correspondence and the BC endomotive over $\F_1$

We now show that not only the BC-endomotive has a model over $\F_1$, but in fact it captures the structure of the extension $\F_{1^\infty}=\varinjlim \F_{1^n}$ over $\F_1$ by means of the Frobenius correspondence.

Theorem 6.3 The structure of the BC-endomotive corresponds to the structure of $\F_{1^\infty}$ over $\F_1$ as follows

a) The abelian part of the BC-endomotive over $\F_1$ corresponds to the inductive system of “extensions” $\F_{1^n}$.
b) The endomorphisms $\sigma_n$ describe the Frobenius correspondence, in the sense that on the algebra $\Z[\Q/\Z]\otimes_\Z \K$, for $\K$ a perfect field of characteristic $p>0$, the endomorphisms $\sigma_n$, $n=p^\ell$ ($\ell\in\N$) coincide with the Frobenius correspondence described in Remark 5.2.

Proof. For a), we recall that the abelian part of the BC-endomotive over $\F_1$ is defined by the projective system $\mu^{(\infty)}$ of algebraic varieties $\mu^{(n)} = \cF\text{Spec}(A_n)$, $A_n = \Z[\Z/(n)]$ cf.(26). By means of the isomorphism of algebras $\Z[T]/(T^n-1) \stackrel{\sim}{\to} A_n$, $u(n)\mapsto e(\frac{1}{n})$ the inductive system of extensions $\F_{1^n}\subset\F_{1^m}$ ($n|m$) corresponds, after extending the coefficients to $\Z$, to the projective limit $\cdots\to\mu^{(m)}\to \mu^{(n)}\to$ which defines geometrically the abelian part of the BC-endomotive. We refer to Section 3 for the details.

For b), we refer to Proposition 5.1. We recall that on an algebraic variety $X_0$ defined over a finite field $\F_q$ ($q=p^\ell$) the Frobenius morphism $\varphi: X_0 \to X_0$ satisfies the property that the composition $\varphi\times\sigma: \bar X_0 \to \bar X_0$, where $\sigma: \bar\F_q \to \bar\F_q$ is the arithmetic Frobenius automorphism, acts on $\bar X_0 := X_0\times \bar\F_q$ by fixing points and by mapping $f\mapsto f^q$ in the structure sheaf of $X_0$. Here, $f^q$ denotes the section $f$ whose coefficients are raised to the $q$-th power. At each fixed level $A_{n}$ of the inductive system of algebras $A_n\otimes_\Z \K$, the endomorphisms $\sigma_k$, for $k = p^\ell$, behave in exactly the same way as the Frobenius homomorphisms (cf.  Proposition 5.1). □

6.3 Recovering the analytic endomotive

In [16], the set of data which define a variety $X$ (of finite type) over $\F_1$ is inclusive of the important analytic information supplied by the assignment of a commutative Banach $\C$-algebra $\cA_X$ (cf. Section 3 of this paper). The definition of $X$ implies that functions of $\cA_X$ can be evaluated at the points of $X$. We shall now show that this analytic part of the set of data which define the BC-system as a pro-variety over $\F_1$ supply naturally the structure of an analytic endomotive in the sense of [4]. The point is that the set-up which describes the pro-variety $\mu^{(\infty)}$ is inclusive of the information supplied by an inductive system of Banach $\C$-algebras $\cA_{\mu^{(n)}}=A_n\otimes_\Z\C$, cf.(19). Taking the inductive limit of these yields the algebra

(102) \[ \cA_{\mu^{(\infty)}}=\varinjlim \cA_{\mu^{(n)}} \]

since the functor $X\mapsto\cA_X$ is contravariant. The following statement is a direct consequence of the construction of the model of the BC-endomotive over $\F_1$ and of (102):

Proposition 6.2 The analytic part of the pro-variety over $\F_1$ associated to the BC endomotive over $\F_1$ coincides with the analytic endomotive of the BC system as described in [4].

Acknowledgment

The authors are partially supported by NSF grants DMS-FRG-0652164, DMS-0652431, and DMS-0651925. The second author gratefully thanks l'Institut des Hautes Études Scientifiques for the hospitality, the pleasant atmosphere and the support received during a visit in January-April 2008. The third author would like to thank Abhijnan Rej for some useful conversations.

References

• Bost, J.B., Connes, A.
  • Hecke algebras, type III factors and phase transitions with spontaneous symmetry breaking in number theory
  • Selecta Math. (N.S.), 1, 411-457 (1995)
  • Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (?!?)
  • View reference in sidebar
• Connes, A.
  • Trace formula in noncommutative geometry and the zeros of the Riemann zeta function
  • Selecta Math. (N.S.), 5, 29-106 (1999)
  • Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (?!?)
  • View reference in sidebar
• Connes, A., Consani, C.
  • On the notion of geometry over $\F_1$
  • Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (?!?)
  • View reference in sidebar
• Connes, A., Consani, C., Marcolli, M.
  • Noncommutative geometry and motives: The thermodynamics of endomotives
  • Adv. Math., 214, 761-831 (2007)
  • Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (?!?)
  • View reference in sidebar
• A. Connes, C. Consani, M. Marcolli
  • The Weil proof and the geometry of the adeles class space, in: Algebra, Arithmetic and Geometry—Manin Festschrift, in: Progr. Math., Birkhäuser
  • 2008, in press, preprint math/0703392
  • Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (?!?)
  • View reference in sidebar
• Connes, A., Marcolli, M.
  • Noncommutative Geometry, Quantum Fields, and Motives
  • Amer. Math. Soc. (2008)
  • Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (?!?)
  • View reference in sidebar
• Consani, C., Marcolli, M.
  • Quantum statistical mechanics over function fields
  • J. Number Theory, 123, 487-528 (2007)
  • Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (?!?)
  • View reference in sidebar
• Deligne, P., Milne, J.S., Ogus, A., Shih, K.
  • Hodge Cycles, Motives, and Shimura Varieties
  • Springer-Verlag, Berlin (1982)
  • Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (?!?)
  • View reference in sidebar
• Durov, N.
  • New approach to Arakelov geometry
  • Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (?!?)
  • View reference in sidebar
• Haran, M.J. Shai
  • Non-additive geometry
  • Compos. Math., 143, 618-688 (2007)
  • Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (?!?)
  • View reference in sidebar
• M. Kapranov, A. Smirnov
  • Cohomology determinants and reciprocity laws
  • unpublished manuscript
  • Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (?!?)
  • View reference in sidebar
• Manin, Y.I.
  • Lectures on zeta functions and motives (according to Deninger and Kurokawa)
  • Astérisque, 228, 121-163 (1995)
  • Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (?!?)
  • View reference in sidebar
• Meyer, R.
  • On a representation of the idele class group related to primes and zeros of L-functions
  • Duke Math. J., 127, 519-595 (2005)
  • Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (?!?)
  • View reference in sidebar
• Pimsner, M.V.
  • A class of $C^*$-algebra generalizing both Cuntz–Krieger algebras and crossed products by Z
  • Free Probability Theory, 189-212 (1997) Fields Inst. Commun., vol. 12, 189-212 (1997)
  • Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (?!?)
  • View reference in sidebar
• C. Soulé
  • On the field with one element, talk given at the Airbeitstagung
  • Bonn, June 1999
  • Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (?!?)
  • View reference in sidebar
• Soulé, C.
  • Les variétés sur le corps à un élément
  • Mosc. Math. J., 4, 217-244 (2004)
  • Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (?!?)
  • View reference in sidebar
• Tate, J.
  • Number theoretic background
  • Automorphic Forms, Representations, and L-Functions, Part 2, 3-26 (1979) Proc. Sympos. Pure Math., vol. 33, 3-26 (1979)
  • Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (?!?)
  • View reference in sidebar
• Tits, J.
  • Sur les analogues algébriques des groupes semi-simples complexes
  • Colloque d'algèbre supérieure, tenu à Bruxelles du 19 au 22 décembre 1956, 261-289 (1957)
  • Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (?!?)
  • View reference in sidebar
• Töen, B., Vaquié, M.
  • Au dessous de $\text{Spec}(\Z)$
  • Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (?!?)
  • View reference in sidebar

• About ScienceDirect
• What is ScienceDirect
• Content details
• Set up
• How to use
• Subscriptions
• Developers

• Contact and support
• Contact and support

• About Elsevier
• About Elsevier
• About SciVerse
• About SciVal
• Terms and Conditions
• Privacy policy
• Information for advertisers